A Python package for barycentric rational approximation
Project description
Barycentric rational approximation 

This is a pure Python package which provides routines for rational and polynomial approximation for real and complex functions through the so-called barycentric representation. The advantage of this representation is (often significantly) improved stability over classical approaches.
See the API documentation for an overview of the available functions.
Features
Best rational approximation using BRASIL
The package implements the novel BRASIL algorithm for best rational approximation; see the paper or the preprint to learn more.
The following example computes the best uniform rational approximation of degree 5 to a given function in the interval [0, pi]:
import numpy as np
import baryrat
def f(x): return np.sin(x) * np.exp(x)
r = baryrat.brasil(f, [0,np.pi], 5)
The rational function r can then be evaluated at arbitrary nodes, its poles computed,
and more. See the documentation for details.
The AAA algorithm
The package includes a Python implementation of the AAA algorithm for rational approximation described in the paper "The AAA Algorithm for Rational Approximation" by Yuji Nakatsukasa, Olivier Sète, and Lloyd N. Trefethen, SIAM Journal on Scientific Computing 2018 40:3, A1494-A1522. (doi)
A MATLAB implementation of this algorithm is contained in Chebfun. The present Python version is a more or less direct port of the MATLAB version.
The "cleanup" feature for spurious poles and zeros is not currently implemented.
Further algorithms
The package includes functions for polynomial interpolation, rational interpolation with either fixed poles or fixed interpolation nodes, Floater-Hormann interpolation, and more.
Extended precision arithmetic
From baryrat 2.1 forward, most functions in the package support computing in extended precision
using the gmpy2 package; linear algebra routines are provided
through the flamp package.
To enable this, first install the flamp package:
pip install flamp
This will automatically install gmpy2 as well if it is not yet installed.
In your code, first set the desired number of decimal digits to compute with by
import flamp
flamp.set_dps(100) # compute with 100 decimal digits precision
Arrays of numbers should be represented as numpy arrays with the object datatype
containing gmpy2 floating point numbers. Some convenience functions to create
such arrays are provided in flamp.
For instance, use flamp.linspace(0, 1, 100) to create equispaced points in
extended precision.
Most functions will autodetect if you pass such extended precision arrays and
use the corresponding extended precision arithmetic in that case. There is
also a use_mp flag for many functions, but it is only required to force
the use of extended precision even when the inputs are in double precision.
Also the BarycentricRational class supports having its nodes, values, and
weights stored in extended precision and will operate accordingly, for instance
when computing the poles.
Installation
The package is implemented in pure Python and depends only on numpy and scipy, with gmpy2 and flamp as optional dependencies as discussed above. Install it using pip:
pip install baryrat
Usage
Here's an example of how to approximate a function in the interval [0,1] using the AAA algorithm:
import numpy as np
from baryrat import aaa
Z = np.linspace(0.0, 1.0, 1000)
F = np.exp(Z) * np.sin(2*np.pi*Z)
r = aaa(Z, F, mmax=10)
Instead of the maximum number of terms mmax, it's also possible to specify
the error tolerance tol. Both arguments work exactly as in the MATLAB
version.
The returned object r is an instance of the class
baryrat.BarycentricRational and can be called like a function. For instance,
you can compute the error on Z like this:
err = F - r(Z)
print(np.linalg.norm(err, np.inf))
If you are interested in the poles and residues of the computed rational function, you can query them like
pol, res = r.polres()
and the zeroes using
zer = r.zeros()
Finally, the nodes, values and weights used for interpolation (called zj,
fj and wj in the original implementation) can be accessed as properties:
r.nodes
r.values
r.weights
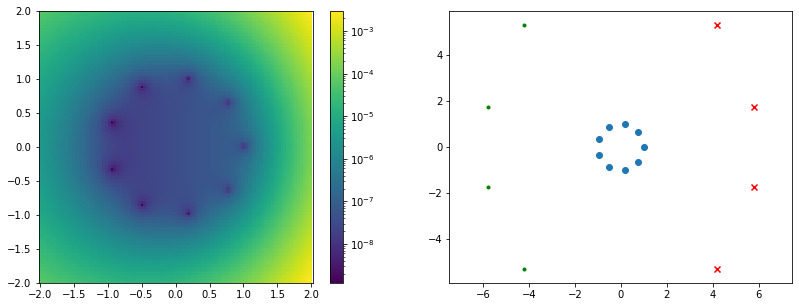
Example: approximating the complex exponential
# create 9 interpolation nodes in a circle
n = 9
nodes = exp(arange(n) / n * 2j * pi)
# interpolate the complex exp function as a degree (4,4) rational function
r = baryrat.interpolate_rat(nodes, exp(nodes))
# compute poles and zeros
poles, zer = r.poles(), r.zeros()
# plot the approximation error and the nodes, poles and zeros
figsize(13.5, 5)
subplot(1, 2, 1)
Y, X = ogrid[-2:2:100j, -2:2:100j]
Z = X + 1j * Y
pcolormesh(X.flat, Y.flat, abs(r(Z) - exp(Z)), norm=mpl.colors.LogNorm())
colorbar();
axis('equal');
subplot(1, 2, 2)
scatter(real(nodes), imag(nodes))
scatter(real(poles), imag(poles), marker='x', c='r')
scatter(real(zer), imag(zer), marker='.', c='g')
axis('equal');
Citing baryrat
If you use this package in any published research, please cite the following publication where the package was first introduced:
- C. Hofreither. An algorithm for best rational approximation based on barycentric rational interpolation. Numerical Algorithms, 88(1):365--388, 2021. (doi)
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file baryrat-2.1.2.tar.gz.
File metadata
- Download URL: baryrat-2.1.2.tar.gz
- Upload date:
- Size: 23.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
815de095b163765b7fa35b9850399e987d030671464c7d7732f97f37b8a8df72
|
|
| MD5 |
b213bfe8abfac60a954585c6d5e853af
|
|
| BLAKE2b-256 |
cee400e84ceb5bb5311e433b41eb8cd5c26061d3a63a5682e102c0161bac5b3c
|
File details
Details for the file baryrat-2.1.2-py3-none-any.whl.
File metadata
- Download URL: baryrat-2.1.2-py3-none-any.whl
- Upload date:
- Size: 18.9 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
3eecb9ff7d31421951172a3fb618e26d40f746bc29cfdd02d71cd768927d42ea
|
|
| MD5 |
1756ce8e0b44244821590a29446a30b0
|
|
| BLAKE2b-256 |
8eb9952899429722c2f2fe243d58100b015dc142c8dbeed6824fc84231499654
|