A Generic Particle+Grid Interface
Project description
GPGI
Fast particle deposition at post-processing time
This small Python library implements fundamental grid deposition algorithms to analyse (rectilinear) grid + particle datasets, with an emphasize on performance. Core algorithms are implemented as Cython extensions.
GPGI stands for Generic Particle + Grid data Interface
Table of Contents
Installation
python -m pip install --upgrade pip
python -m pip install gpgi
Supported applications
A rectilinear grid is defined as 1D arrays representing cell left edges in each directions. Note that the last point of such an array is interpreted as the right edge of the rightmost cell, so for instance, a 1D grid containing 100 cells is defined by 101 edges.
Particles are defined as points that live within the grid's bounds.
Deposition is the action of going from particle description to a grid description of a field. It is useful to analyze, compare and combine simulation data that exists in a combination of the two formalisms. This process is not reversible as it degrades information.
For instance, here's a simple overlay of a particle set (red dots) against a background that represents the deposited particle count.
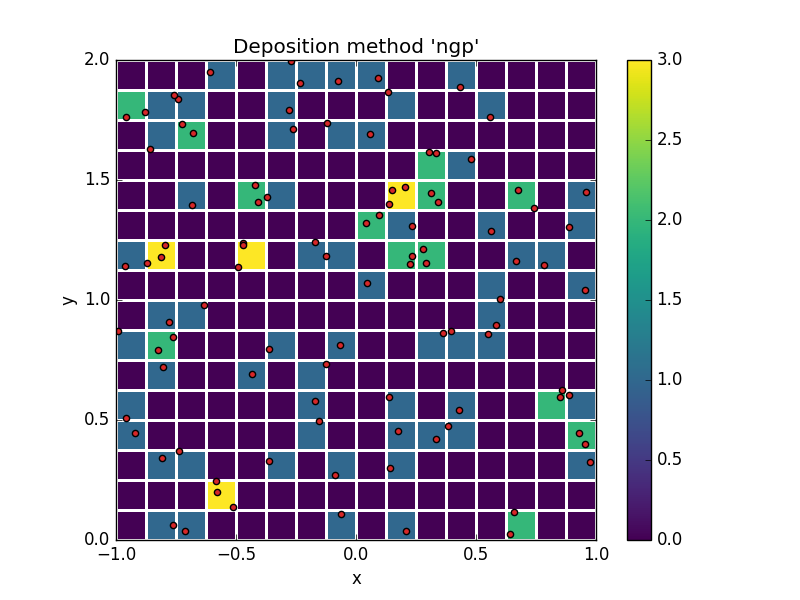
This example illustrates the simplest possible deposition method, "Nearest Grid Point" (NGP), in which each particle contributes only to the cell that contains it.
More refined methods are also available.
Builtin deposition methods
| method name | abbreviated name | order |
|---|---|---|
| Nearest Grid Point | NGP | 0 |
| Cloud in Cell | CIC | 1 |
| Triangular Shaped Cloud | TSC | 2 |
new in gpgi 0.12.0
User-defined alternative methods may be provided to Dataset.deposit as method=my_func.
Their signature need to be compatible with gpgi.typing.DepositionMethodT or gpgi.typing.DepositionMethodWithMetadataT .
Supported geometries
| geometry name | axes order |
|---|---|
| cartesian | x, y, z |
| polar | radius, z, azimuth |
| cylindrical | radius, azimuth, z |
| spherical | radius, colatitude, azimuth |
| equatorial | radius, azimuth, latitude |
Time complexity
An important step in performing deposition is to associate particle indices to cell indices. This step is called "particle indexing". In directions where the grid is uniformly stepped (if any), indexing a particle is an O(1) operation. In the more general case, indexing is performed by bisection, which is a O(log(nx)) operation (where nx represents the number of cells in the direction of interest).
Usage
The API consists in a load function, which returns a Dataset object.
Load data
import numpy as np
import gpgi
nx = ny = 64
nparticles = 600_000
prng = np.random.RandomState(0)
ds = gpgi.load(
geometry="cartesian",
grid={
"cell_edges": {
"x": np.linspace(-1, 1, nx),
"y": np.linspace(-1, 1, ny),
},
},
particles={
"coordinates": {
"x": 2 * (prng.normal(0.5, 0.25, nparticles) % 1 - 0.5),
"y": 2 * (prng.normal(0.5, 0.25, nparticles) % 1 - 0.5),
},
"fields": {
"mass": np.ones(nparticles),
},
},
)
The Dataset object holds a grid and a particles attribute,
which both hold a fields attribute for accessing their data.
But more importantly, the Dataset has a deposit method to
translate particle fields to the grid formalism.
Deposit Particle fields on the grid
particle_mass = ds.deposit("mass", method="nearest_grid_point") # or "ngp" for shorts
Visualize
In this example we'll use matplotlib for rendering, but note that matplotlib is not a dependency to gpgi
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.set(aspect=1, xlabel="x", ylabel="y")
im = ax.pcolormesh(
"x",
"y",
particle_mass.T,
data=ds.grid.cell_edges,
cmap="viridis",
)
fig.colorbar(im, ax=ax)
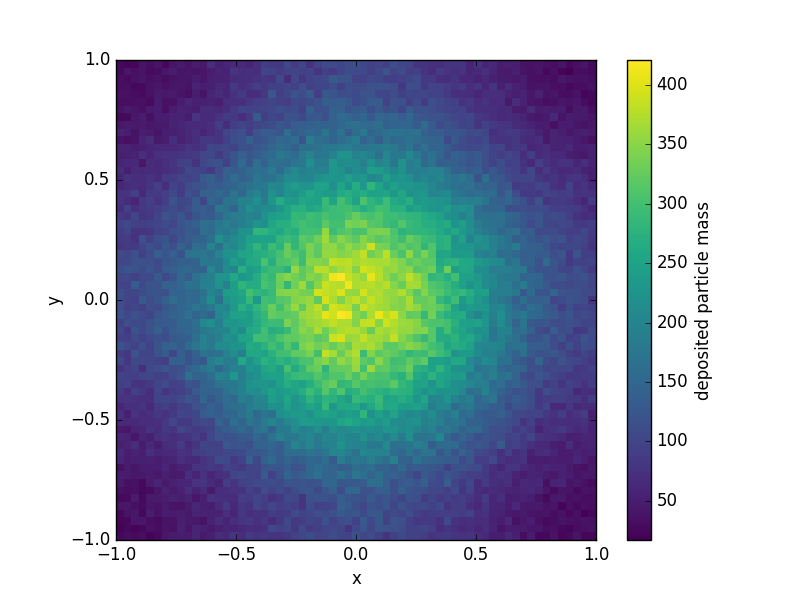
The example script given here takes about a second (top to bottom).
Supplying arbitrary metadata
new in gpgi 0.4.0
Dataset objects have a special attribute metadata which is a dictionary with string keys.
This attribute is meant to hold any special metadata that may be relevant for labelling or processing (e.g. simulation time, author, ...).
Metadata can be supplied at load time as
ds = gpgi.load(
geometry="cartesian",
grid=...,
particles=...,
metadata={"simulation_time": 12.5, "author": "Clément Robert"}
)
Boundary conditions
new in gpgi 0.5.0
With CIC and TSC deposition, particles contribute to cells neighbouring the one
that contains them. For particles that live in the outermost layer of the
domain, this means some of their contribution is lost. This behavior
corresponds to the default 'open' boundary condition, but gpgi has builtin
support for more conservative boundary conditions.
Boundary conditions can selected per field, per axis and per side. Builtin recipes all perform linear combinations of ghost layers (same-side and opposite side) and active domain layers (same-side and opposite side), and replace the same-side active layer with the result.
User-selected boundary conditions take the form of an optional argument to
Dataset.deposit, as dictionary with keys being axes names, and values being
2-tuples of boundary conditions names (for left and right side respectively).
For instance, here's how one would require periodic boundary conditions on all axes:
ds.deposit(
"mass",
method="cic",
boundaries={
"x": ("periodic", "periodic"),
"y": ("periodic", "periodic"),
}
)
Unspecified axes will use the default 'open' boundary.
Builtin recipes
| boundary conditions | description | conservative ? |
|---|---|---|
| open (default) | no special treatment | no |
| periodic | add opposite ghost layer to the active domain | yes |
| wall | add same-side ghost layer to the active domain | yes |
| antisymmetric | subtract same-side ghost layer from the active domain | no |
Define custom recipes
gpgi's boundary recipes can be customized. Let's illustrate this feature with a simple example.
Say we want to fix the value of the deposited field in some outer layer.
This is done by defining a new function on the user side:
def ones(
same_side_active_layer,
same_side_ghost_layer,
opposite_side_active_layer,
opposite_side_ghost_layer,
weight_same_side_active_layer,
weight_same_side_ghost_layer,
weight_opposite_side_active_layer,
weight_opposite_side_ghost_layer,
side,
metadata,
):
return 1.0
where all first eight arguments are numpy.ndarray objects with the same shape (which includes ghost padding !),
to which the return value must be broadcastable, side can only be either
"left" or "right", and metadata is the special Dataset.metadata
attribute. Not all arguments need be used in the body of the function, but this
signature is required.
The method must then be registered as a boundary condition recipe as
ds.boundary_recipes.register("ones", ones)
where the associated key (here "ones") is arbitrary. The recipe can now be
used exactly as builtin ones, and all of them can be mixed arbitrarily.
ds.deposit(
"mass",
method="cic",
boundaries={
"x": ("ones", "wall"),
"y": ("periodic", "periodic"),
}
)
Note that all first eight arguments in a boundary recipe function should
represent an extensive physical quantity (as opposed to intensive). When
depositing an intensive quantity u, a weight field w should be supplied
(see next section), in which case, the first four arguments represent u*w and
the following four represent w, so that u can still be obtained within the
function as a ratio if needed.
Weight fields (Depositing intensive quantities)
new in gpgi 0.7.0
Fundamentally, deposition algorithms construct on-grid fields by performing summations. An implication is that the physical quantities being deposited are required to be extensive (like mass or momentum). Intensive quantities (like velocity or temperature) require additional operations, and necessitate the use of an additional weight field.
This section provides showcases their usage. For a detailed explanation of the deposition algorithm for intensive quantities, see Deposition algorithm.
In order to deposit an intensive field (e.g., vx), an additional weight_field argument must be provided as
ds.deposit(
"vx",
method="cic",
boundaries={
"y": ("periodic", "periodic"),
"x": ("antisymmetric", "antisymmetric"),
},
weight_field="mass",
weight_field_boundaries={
"y": ("periodic", "periodic"),
"x": ("open", "open"),
},
)
Boundary recipes may be also associated to the weight field with the
weight_field_boundaries argument. This arguments becomes required if
boundaries and weight_field are both provided.
Call help(ds.deposit) for more detail.
Count Sorting
new in gpgi 0.14.0
gpgi can load arbitrarily ordered particle sets, though deposition algorithms perform better when the in-memory position of particles correlates with their physical positions relative to the grid, since such a state minimizes the number of cache misses.
Particles may be sorted by a counting sort algorithm, as
ds = ds.sorted()
Note that this method returns a copy of the dataset, so it will best perform for datasets that, at most, fit in half your RAM.
This operation is costly in itself, so there may be a trade-off depending on how many depositions one needs to perform on a given dataset before tossing it out.
By default, axes are weighted in the order that's optimal for gpgi's deposition routines, but arbitrary priority order may be specified as, for instance
ds = ds.sorted(axes=(1, 0))
Use the Dataset.is_sorted method to check whether particles are already sorted without
performing the sort. Dataset.is_sorted accepts an axes argument just like Dataset.sorted. This is useful for testing and comparative purposes.
Deposition algorithm
This section provides details on the general deposition algorithm, as
implemented in gpgi.
Without loss of generality, we will illustrate how an intensive field (v)
is deposited, since this case requires the most computational steps. As it
happens, depositing an extensive field (w) separately is actually part of
the algorithm.
Definitions
vis an intensive field that we want to deposit on the gridwis an extensive field that will be used as weightsu = v * wis an extensive equivalent tov(conceptually, ifvis a velocity andwis a mass,ucorresponds to a momentum)
u(i), v(i) and w(i) are defined for each particle i.
We note U(x), V(x) and W(x) the corresponding on-grid fields, where V(x)
is the final output of the algorithm. These are defined at grid cell centers
x, within the active domain.
Last, we note U'(x), V'(x) and W'(x) the raw deposited fields, meaning
no special treatment is applied to the outermost layers (boundary conditions).
These are defined at grid cell centers, including one ghost layer that will be
used to apply boundary conditions.
Algorithm
W'andU'are computed as
W'(x) = Σ c(i,x) w(i)
U'(x) = Σ c(i,x) w(i) v(i)
where c(i,x) are geometric coefficients associated with the deposition method. Taking the nearest grid point (NGP) method for illustration, c(i,x) = 1 if particle i is contained in the cell whose center is x, and c(i,x) = 0 elsewhere.
- boundary conditions are applied
W(x) = W_BCO(W', 1, metadata)
U(x) = U_BCO(U', W', metadata)
where W_BCO and U_BCO denote arbitrary boundary condition operators
associated with W and U respectively, and which take 3 arguments,
representing the field to be transformed, its associated weight field and a
wildcard metadata argument which may contain any additional data relevant to
the operator.
Note 1 is used a placeholder "weight" for W, for symmetry reasons: all boundary condition operators must expose a similar interface, as explained in Define custom recipes.
- Finally,
V(x)is obtained as
V(x) = (U/W)(x)
Thread safety
Starting in gpgi 2.0.0, thread safety is guaranteed in Dataset.host_cell_index
computation and Dataset.deposit, and both operations release the
GIL (Global Interpreter Lock) around their respective hotloops. Thread safety is
also tested against the experimental free-threaded build of Python 3.13.
Note that, by default, Dataset.deposit still uses a lock per Dataset
instance, which in the most general case is preferable since concurrently
depositing many fields can cause catastrophic degradations of performances as
it encourages cache misses. Optimal performance is however application-specific,
so this strategy can be overridden using the lock parameter:
- using
lock=Nonewill not use any lock, which in restricted conditions leads to better walltime performances - alternatively, an externally managed
threading.Lockinstance may be supplied
Dataset.boundary_recipes.register is also thread-safe: registering a shared
function multiple times is supported, but an error is raised in case one
attempts registering a different function under an existing key.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distributions
File details
Details for the file gpgi-2.0.0.tar.gz.
File metadata
- Download URL: gpgi-2.0.0.tar.gz
- Upload date:
- Size: 46.4 kB
- Tags: Source
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
c98e6b06dd42e5ce333e6346ca113ca5f6316457f85e7bd78ebe763441825d67
|
|
| MD5 |
2f13a61378f691e92a3d39cbd6ecb1f4
|
|
| BLAKE2b-256 |
9d486c8833406d5cc8d1ec6d85302d73acdad1d1776c30076d6adb3ca784d5f9
|
File details
Details for the file gpgi-2.0.0-cp313-cp313-win_amd64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp313-cp313-win_amd64.whl
- Upload date:
- Size: 182.5 kB
- Tags: CPython 3.13, Windows x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
d6e7197bc9aa52f9654cf736e4bbbb56f0d67fb2ac7f6d1c4b198e75cf2d722b
|
|
| MD5 |
f0bb670c9c564bb376144adad0f206ac
|
|
| BLAKE2b-256 |
65c1b2726435e304ea3d86ec7b8240a4a6f366df5c43899487c657c1533eae86
|
File details
Details for the file gpgi-2.0.0-cp313-cp313-musllinux_1_2_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp313-cp313-musllinux_1_2_x86_64.whl
- Upload date:
- Size: 1.2 MB
- Tags: CPython 3.13, musllinux: musl 1.2+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
6f3a1b5dcdb32052149fa2bfeac1c840bd95bd13ee32495da70646bdd3180872
|
|
| MD5 |
5b758f443211c98591c124291a4f78af
|
|
| BLAKE2b-256 |
dbcd4b8dbf747490e215dcbdd082acbfcc2046daf33d41f56221612a7b94b0ae
|
File details
Details for the file gpgi-2.0.0-cp313-cp313-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp313-cp313-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 1.2 MB
- Tags: CPython 3.13, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
b4e3c7c59f4afd133af39ca1df30314b96dd9cec1889df434b64115b9b374591
|
|
| MD5 |
76b88aca16dce5ca74e8386ca35b0fa0
|
|
| BLAKE2b-256 |
d85fd4a37dea0c94a0ad1cc585a3d89707f39d11e3851821c0145630966142e5
|
File details
Details for the file gpgi-2.0.0-cp313-cp313-macosx_11_0_arm64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp313-cp313-macosx_11_0_arm64.whl
- Upload date:
- Size: 171.3 kB
- Tags: CPython 3.13, macOS 11.0+ ARM64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
35957754e69034bf5c89a0a18fd1c2b88e00fdf130bcb15d2709c1b18a543994
|
|
| MD5 |
a6a6cda7269554a6025790000dd56892
|
|
| BLAKE2b-256 |
14af464bf1bd0ecc96fb6fe59742234281c26cdb2557709e91661bde2735c9fb
|
File details
Details for the file gpgi-2.0.0-cp313-cp313-macosx_10_13_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp313-cp313-macosx_10_13_x86_64.whl
- Upload date:
- Size: 203.3 kB
- Tags: CPython 3.13, macOS 10.13+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
5578ea252fa9f9c79b6f1cbcce30ba7797125f2d15e304fb9ae626d4816446d6
|
|
| MD5 |
999f9e98759e33897009f082ae75123f
|
|
| BLAKE2b-256 |
8e58b1721124999309de28a6bc072821f73a08107b2047b338740a1a06433095
|
File details
Details for the file gpgi-2.0.0-cp312-cp312-win_amd64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp312-cp312-win_amd64.whl
- Upload date:
- Size: 182.4 kB
- Tags: CPython 3.12, Windows x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
8682653f00e8459b16d3b8c3ea1b0a3a3738ae389f63c1160fe50b520882de2a
|
|
| MD5 |
07277be0a58c24514048b701ebe74d79
|
|
| BLAKE2b-256 |
215afe1b9ddc01d3e89e2c2a8f8aeb2ec9efee40ef314e4fcd06e5da9e5d2fa5
|
File details
Details for the file gpgi-2.0.0-cp312-cp312-musllinux_1_2_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp312-cp312-musllinux_1_2_x86_64.whl
- Upload date:
- Size: 1.2 MB
- Tags: CPython 3.12, musllinux: musl 1.2+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
033bca7b96540db659fcbc3f48da242332a672a3af0e8f04bb4f1f24a6873360
|
|
| MD5 |
d12f14b6d137c4314be132da6ac8237e
|
|
| BLAKE2b-256 |
d585ed2dedcae8ce175c21001bea8da28bbd2bf36c417914720a898a2fac87f5
|
File details
Details for the file gpgi-2.0.0-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp312-cp312-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 1.2 MB
- Tags: CPython 3.12, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
baf7dbdfe42ba8aabd638456dd5f8dfb6a90e816b9f4a3d10e1c4f0cc8559fa6
|
|
| MD5 |
b5ea2c9a3297adfc6b663897eb698454
|
|
| BLAKE2b-256 |
084557c3c65dfc79d75980c02e431c9525ab7b79b8afae80b814fc4195b894e8
|
File details
Details for the file gpgi-2.0.0-cp312-cp312-macosx_11_0_arm64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp312-cp312-macosx_11_0_arm64.whl
- Upload date:
- Size: 171.9 kB
- Tags: CPython 3.12, macOS 11.0+ ARM64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
1cd229779fa042752027c80521a22f58ef336396357efc2567ce61002394a39e
|
|
| MD5 |
fe2bd9acbd065353f31037fd89d049a9
|
|
| BLAKE2b-256 |
a4e4d180868da265d7c7d8298b0a72d435bdbcc281356852517dfb670cbbec52
|
File details
Details for the file gpgi-2.0.0-cp312-cp312-macosx_10_13_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp312-cp312-macosx_10_13_x86_64.whl
- Upload date:
- Size: 206.0 kB
- Tags: CPython 3.12, macOS 10.13+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
65c62c94fd9f0f23110d76be08249577a422710aa5b206c627d6e3ca8420f868
|
|
| MD5 |
d03f001ee27fbb7fdd6b141aee977fe7
|
|
| BLAKE2b-256 |
bb9dda89253d3b4490cb55ee4132ceb635c9f73627214b66dc27b83a3b2a7b47
|
File details
Details for the file gpgi-2.0.0-cp311-cp311-win_amd64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp311-cp311-win_amd64.whl
- Upload date:
- Size: 179.6 kB
- Tags: CPython 3.11, Windows x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
922c6654fc4afb569a961f8f21f9c8fe2fbbbc179dd2fc122a06b8d67cb69d15
|
|
| MD5 |
b10a6da0955d78ceb5ad527e3a9c4d4b
|
|
| BLAKE2b-256 |
38996018cb2ee81b7f995950628c868151a8b93f0fba30cb1ccbf55c9704e9cf
|
File details
Details for the file gpgi-2.0.0-cp311-cp311-musllinux_1_2_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp311-cp311-musllinux_1_2_x86_64.whl
- Upload date:
- Size: 1.3 MB
- Tags: CPython 3.11, musllinux: musl 1.2+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
d6efd1dbdb56bcabd80bf3d2d0ecafaf78d76b165e04c71dcef3fcf426486a33
|
|
| MD5 |
6587d66bcaa63a1bc119f59e030bc3be
|
|
| BLAKE2b-256 |
7c6c96e92ce029d7acefeed8dfe6d341f834910beb98e6cb734568ec9a1be4f3
|
File details
Details for the file gpgi-2.0.0-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl
- Upload date:
- Size: 1.2 MB
- Tags: CPython 3.11, manylinux: glibc 2.17+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
71a835ff50819db7b2b2c2b011ff332e04cb0e1761f7efb185b4625da6429d17
|
|
| MD5 |
fb8f1f31b1c27e127e703f6f7a1859fd
|
|
| BLAKE2b-256 |
fe32ee62eb3dc10b9854729ae25a98d312ef25ae3d3e3f8feb4f36dae6ce7659
|
File details
Details for the file gpgi-2.0.0-cp311-cp311-macosx_11_0_arm64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp311-cp311-macosx_11_0_arm64.whl
- Upload date:
- Size: 169.6 kB
- Tags: CPython 3.11, macOS 11.0+ ARM64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
e30acd3055355ede823b2cdbe8f47056ad94a1f857c68d056fb284beeb4e4002
|
|
| MD5 |
e5f9ca1d5c8388e421ecdc807a518296
|
|
| BLAKE2b-256 |
ec9ddd2a1df050a3018e8e046047f461c76945455fb0a946a746163210f4231c
|
File details
Details for the file gpgi-2.0.0-cp311-cp311-macosx_10_9_x86_64.whl.
File metadata
- Download URL: gpgi-2.0.0-cp311-cp311-macosx_10_9_x86_64.whl
- Upload date:
- Size: 198.2 kB
- Tags: CPython 3.11, macOS 10.9+ x86-64
- Uploaded using Trusted Publishing? Yes
- Uploaded via: twine/5.1.1 CPython/3.12.7
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
cee4af4a456520cbdccc82ecf8c63ab9c5c04feac508fd773cd1f046c2b42037
|
|
| MD5 |
507cf3288faba1bcf635eee1a9a70f40
|
|
| BLAKE2b-256 |
c34dd91caf2551457a706b5d6dc5b13f79dbe3656cc3976d2497b51f0eb7871f
|













