Knee-point detection in Python
Project description
kneed
Knee-point detection in Python
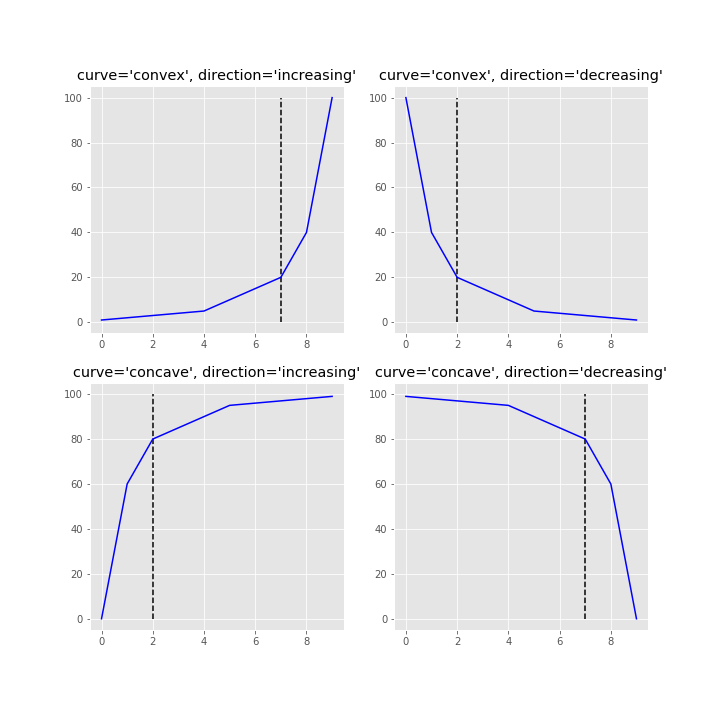
This repository is an attempt to implement the kneedle algorithm, published here. Given a set of x and y values, kneed will return the knee point of the function. The knee point is the point of maximum curvature.
Table of contents
Installation
kneed has been tested with Python 3.7, 3.8, 3.9, and 3.10.
anaconda
$ conda install -c conda-forge kneed
pip
$ pip install kneed # To install only knee-detection algorithm
$ pip install kneed[plot] # To also install plotting functions for quick visualizations
Clone from GitHub
$ git clone https://github.com/arvkevi/kneed.git && cd kneed
$ pip install -e .
Usage
These steps introduce how to use kneed by reproducing Figure 2 from the manuscript.
Input Data
The DataGenerator class is only included as a utility to generate sample datasets.
Note:
xandymust be equal length arrays.
from kneed import DataGenerator, KneeLocator
x, y = DataGenerator.figure2()
print([round(i, 3) for i in x])
print([round(i, 3) for i in y])
[0.0, 0.111, 0.222, 0.333, 0.444, 0.556, 0.667, 0.778, 0.889, 1.0]
[-5.0, 0.263, 1.897, 2.692, 3.163, 3.475, 3.696, 3.861, 3.989, 4.091]
Find Knee
The knee (or elbow) point is calculated simply by instantiating the KneeLocator class with x, y and the appropriate curve and direction.
Here, kneedle.knee and/or kneedle.elbow store the point of maximum curvature.
kneedle = KneeLocator(x, y, S=1.0, curve="concave", direction="increasing")
print(round(kneedle.knee, 3))
0.222
print(round(kneedle.elbow, 3))
0.222
The knee point returned is a value along the x axis. The y value at the knee can be identified:
print(round(kneedle.knee_y, 3))
1.897
Visualize
The KneeLocator class also has two plotting functions for quick visualizations.
Note that all (x, y) are transformed for the normalized plots
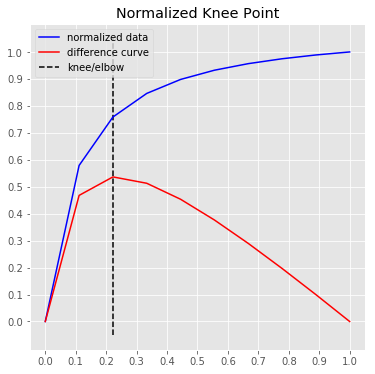
# Normalized data, normalized knee, and normalized distance curve.
kneedle.plot_knee_normalized()
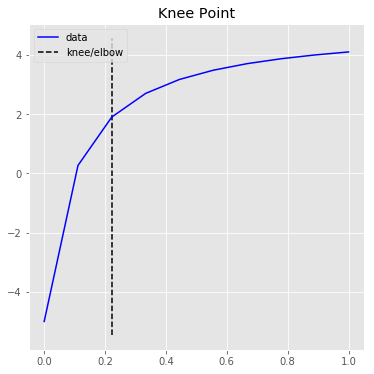
# Raw data and knee.
kneedle.plot_knee()
Documentation
Documentation of the parameters and a full API reference can be found here.
Interactive
An interactive streamlit app was developed to help users explore the effect of tuning the parameters. There are two sites where you can test out kneed by copy-pasting your own data:
You can also run your own version -- head over to the source code for ikneed.
Contributing
Contributions are welcome, please refer to CONTRIBUTING to learn more about how to contribute.
Citation
Finding a “Kneedle” in a Haystack: Detecting Knee Points in System Behavior Ville Satopa † , Jeannie Albrecht† , David Irwin‡ , and Barath Raghavan§ †Williams College, Williamstown, MA ‡University of Massachusetts Amherst, Amherst, MA § International Computer Science Institute, Berkeley, CA
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file kneed-0.8.5.tar.gz.
File metadata
- Download URL: kneed-0.8.5.tar.gz
- Upload date:
- Size: 12.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.4
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
a4847ac4f1d04852fea278d5de7aa8bfdc3beb7fbca4a182fec0f0efee43f4b1
|
|
| MD5 |
83cdebc06cf91ef8d71d29383c3733ac
|
|
| BLAKE2b-256 |
ba0f958e27a378042e0366dfea8baab4a53121cb37c114117666051390cd7bb8
|
File details
Details for the file kneed-0.8.5-py3-none-any.whl.
File metadata
- Download URL: kneed-0.8.5-py3-none-any.whl
- Upload date:
- Size: 10.3 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.2 CPython/3.11.4
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
2f3fbd4e9bd808e65052841448702c41ea64d5fc78735cbfc97ab25f08bd9815
|
|
| MD5 |
83e90dfba941e30701c9747639c02733
|
|
| BLAKE2b-256 |
9a1b7e726d8616e813007874468c61790099ba21493e0ea07561b7d9fc53151c
|