Tool for optimizing dynamic systems using direct collocation.
Project description
PyPi |


|
Anaconda |


|
Documentation |

|
JOSS Paper |

|
Zenodo Archive |

|
Continous Integration |

|
Introduction
opty utilizes symbolic descriptions of differential algebraic equations expressed with SymPy to form the constraints needed to solve optimal control and parameter identification problems using the direct collocation method and non-linear programming (NLP). In general, if one can express the continuous first order differential algebraic equations of the system as symbolic expressions opty will automatically generate a function to efficiently evaluate the dynamical constraints and a function that evaluates the sparse Jacobian of the constraints, which have been optimized for speed and memory consumption. The translation of the dynamical system description to the NLP form, primarily the formation of the constraints and the Jacobian of the constraints, manually is a time consuming and error prone process. opty eliminates both of those issues.
opty uses its primary dependencies in the following ways:
SymPy: Symbolically discretizes the DAEs, analytically computes all necessary derivatives, and generates C code to efficiently evaluate the DAEs and their associated derivatives.
Cython + NumPy: Just-In-Time compiles the C code generated by SymPy and wraps it for use with NumPy arrays.
cyipopt: Wraps the Ipopt C API and provides a generic NLP problem definition class which opty’s problem class is derived from to facilitate input and output from Ipopt as NumPy arrays.
Ipopt: Consumes the numerical problem definition passed via cyipopt and then solves it using an interior point method.
Features
Both implicit and explicit forms of the first order ordinary differential equations and differential algebraic equations are supported, i.e. there is no need to solve for the derivatives of the dependent variables.
Backward Euler or Midpoint integration methods.
Supports both trajectory optimization and parameter identification, independently or simultaneously.
Solve fixed duration or variable duration problems.
Easy specification of bounds on free variables.
Easily specify additional “instance” constraints.
Efficient numerical execution of large equations of motion.
Automatic parallel execution using openmp if installed.
Built with support of sympy.physics.mechanics and PyDy in mind.
Example Solutions
Animations from some of the examples.
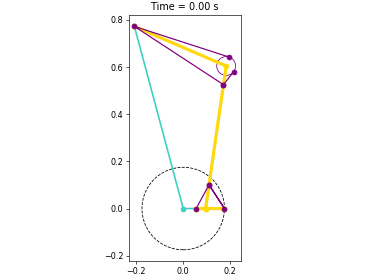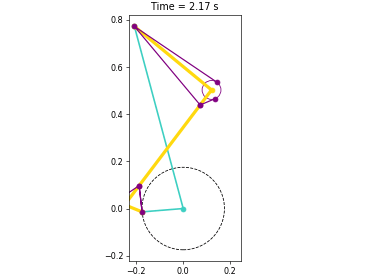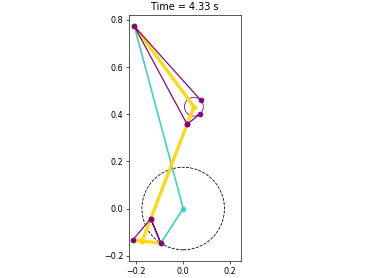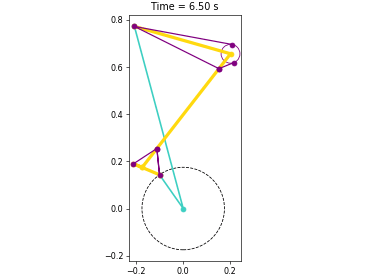
|
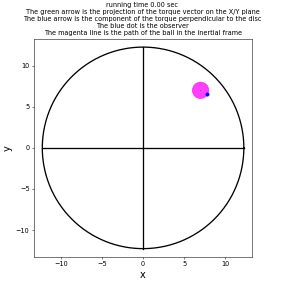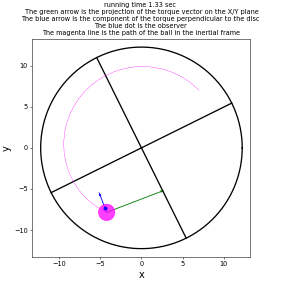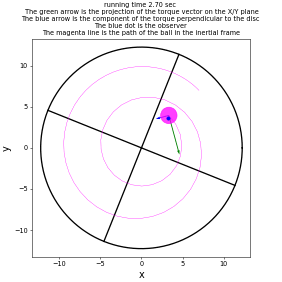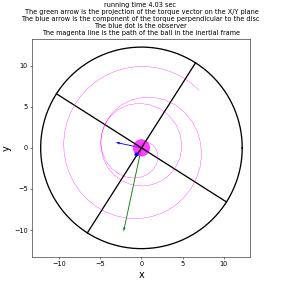
|
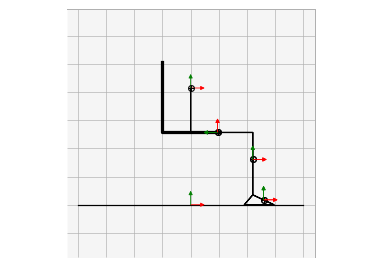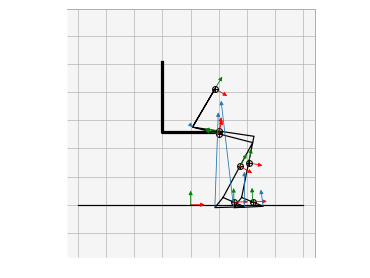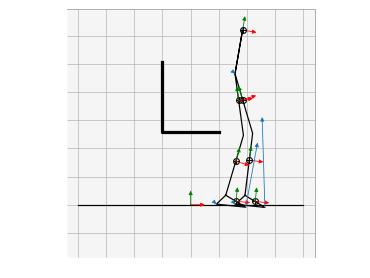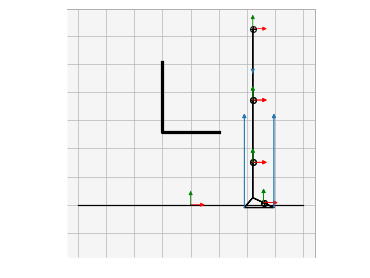
|
|
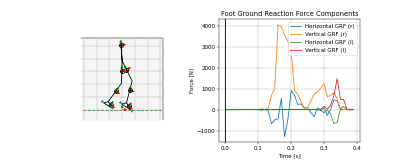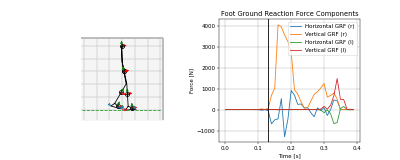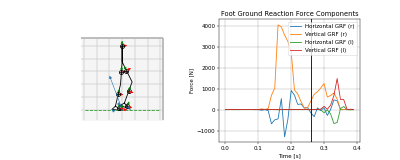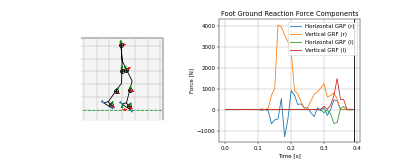
|
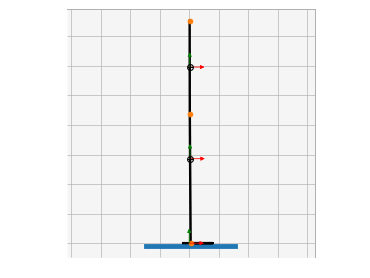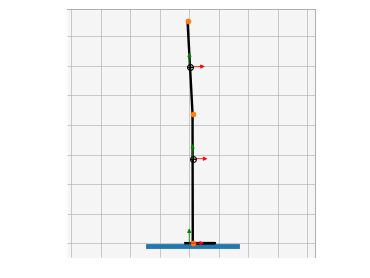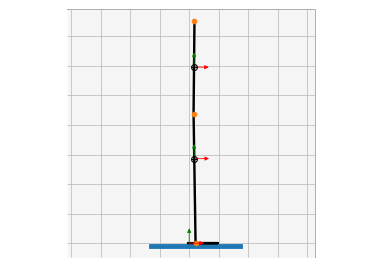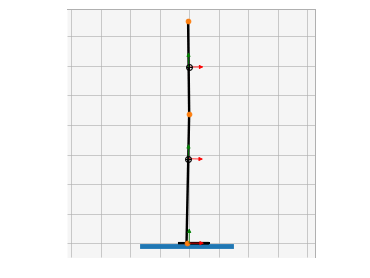
|
Installation
The required dependencies are as follows:
cyipopt >= 1.1.0 [with ipopt >= 3.11 (Linux & OSX), >= 3.13 (Windows)]
cython >= 0.29.19 [with a C compiler]
numpy >= 1.19.0
python 3.9-3.13
setuptools
sympy >= 1.6.0
The optional dependencies are as follows:
matplotlib >= 3.2.0
openmp
scipy >= 1.5.0
To run all of the examples the following additional dependencies may be needed:
gait2d
pandas
pydy >= 0.5.0
pytables
pyyaml
symmeplot
yeadon
The easiest way to install opty is to first install Anaconda (or Miniconda or Miniforge) and use the conda package manager to install opty and any desired optional dependencies from the Conda Forge channel, e.g. opty:
$ conda install --channel conda-forge opty
and the optional dependencies:
$ conda install --channel conda-forge matplotlib openmp scipy
Opty can be installed with pip, but this will require installing and compiling cyipopt if it is not already installed:
$ pip install opty
See the cyipopt documentation for information on installing that package.
There are also several dependency groups:
$ pip install opty[optional] # use extra functionality in opty $ pip install opty[examples] # run all example scripts $ pip install opty[doc] # build the documentation
Custom Ipopt
If you want a custom installation of any of the dependencies, e.g. Ipopt, you must first install Ipopt along with it’s headers. For example, on Debian based systems you can use the package manager:
$ sudo apt-get install coinor-libipopt1v5 coinor-libipopt-dev
or prebuilt binaries can be downloaded from https://www.coin-or.org/download/binary/Ipopt/.
For customized installation (usually desired for performance) follow the instructions on the Ipopt documentation to compile the library. If you install to a location other than /usr/local on Unix systems you will likely have to set the LD_LIBRARY_PATH so that you can link to Ipopt when installing cyipopt.
Once Ipopt is installed and accessible, install conda then create an environment:
$ conda create -n opty-custom -c conda-forge cython numpy pip setuptools sympy $ source activate opty-custom (opty-custom)$ pip install cyipopt # this will compile cyipopt against the available ipopt (opty-custom)$ pip install opty
If you want to develop opty, create a conda environment with all of the development dependencies installed:
$ cd /path/to/opty/ $ conda env create -f opty-dev-env.yml $ conda activate opty-dev
Next install the development version of opty with:
(opty-dev)$ python -m pip install --no-deps --no-build-isolation --editable .
Usage
There are several examples available in the examples directory and the examples-gallery/beginner, examples-gallery/intermediate and examples-gallery/advanced directories. The optimal torque to swing up a pendulum with minimal energy can be run with:
$ python examples-gallery/beginner/plot_pendulum_swing_up_fixed_duration.py
Failed Compilation
If compilation fails it may be helpful to manually compile the generated Cython extension. To do so, provide a destination path to the tmp_dir kwarg when you instantiate Problem(), e.g.:
p = Problem(..., tmp_dir='opty_source')You can then compile the files manually by navigating into the opty_source directory and running:
$ cd /path/to/opty_source $ python ufuncify_matrix_X_setup.py build_ext --inplace
The highest integer value of X will be the most recently generated set of source files.
Build Documentation
Build the HTML documentation with:
(opty-dev)$ cd /path/to/opty/docs (opty-dev)$ make html
and open the result with your web browser, for example:
$ firefox _build/html/index.html
Alternatively, in the windows explorer open opyt/docs/_build/html/index.html.
Acknowledgements
opty was created to generalize and make more accessible the optimal control methods Prof. Ton van den Bogert and his collaborators developed and use for investigating control of musculoskeletal models. His pioneering work and help made the development of opty possible.
Funding
The work was partially funded by the State of Ohio Third Frontier Commission through the Wright Center for Sensor Systems Engineering (WCSSE), by the USA National Science Foundation under Grant No. 1344954, and by National Center of Simulation in Rehabilitation Research 2014 Visiting Scholarship at Stanford University, and the CZI grant CZIF2021-006198 and grant DOI https://doi.org/10.37921/240361looxoj from the Chan Zuckerberg Initiative Foundation (funder DOI 10.13039/100014989).
Project details
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file opty-1.4.0.tar.gz.
File metadata
- Download URL: opty-1.4.0.tar.gz
- Upload date:
- Size: 324.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.11.10
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
5d814c4d592276d8abae559bfc2bd6eb5bcdba863deb7ece0672cf79b0a159ab
|
|
| MD5 |
dfddde0040c871fa23ce9ad9d1532a11
|
|
| BLAKE2b-256 |
e3fc563813635954a1dbf6ec6fec5a0da09a774f5076a0ba2fe3c7f0176643a0
|










