pca: A Python Package for Principal Component Analysis.
Project description

pca is a Python package for Principal Component Analysis. The core of PCA is built on sklearn functionality to find maximum compatibility when combining with other packages.
But this package can do a lot more. Besides the regular PCA, it can also perform SparsePCA, and TruncatedSVD. Depending on your input data, the best approach can be chosen.
pca contains the most-wanted analysis and plots. Navigate to API documentations for more detailed information. ⭐️ Star it if you like it ⭐️
Key Features
| Feature | Description | Docs | Medium | Gumroad & Podcast |
|---|---|---|---|---|
| Fit and Transform | Perform the PCA analysis. | Link | PCA Guide | Link |
| Biplot and Loadings | Make Biplot with the loadings. | Link | – | – |
| Explained Variance | Determine the explained variance and plot. | Link | – | – |
| Best Performing Features | Extract the best performing features. | Link | – | – |
| Scatterplot | Create scatterplot with loadings. | Link | – | – |
| Outlier Detection | Detect outliers using Hotelling T2 and/or SPE/Dmodx. | Link | Outlier Detection | Link |
| Normalize out Variance | Remove any bias from your data. | Link | – | – |
| Save and load | Save and load models. | Link | – | – |
| Analyze discrete datasets | Analyze discrete datasets. | Link | – | – |
Resources and Links
- Example Notebooks: Examples
- Medium Blogs Medium
- Gumroad Blogs with podcast: GumRoad
- Documentation: Website
- Bug Reports and Feature Requests: GitHub Issues
Installation
pip install pca
from pca import pca
Examples
| Quick Start | Make Biplot |
|---|---|
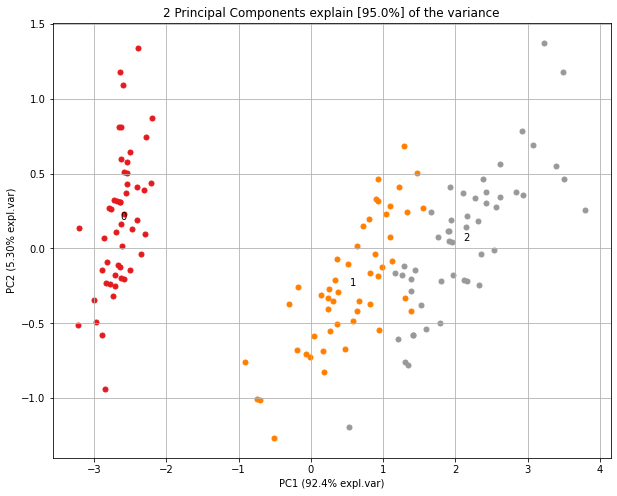
|
|
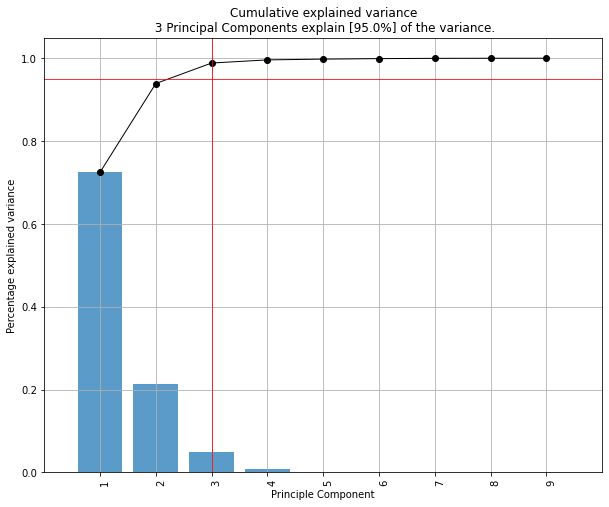
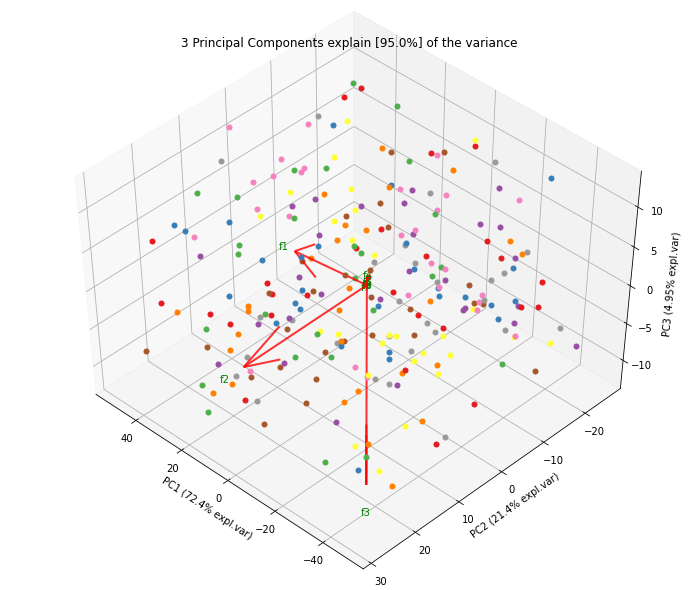
| Explained Variance Plot | 3D Plots |

|

|
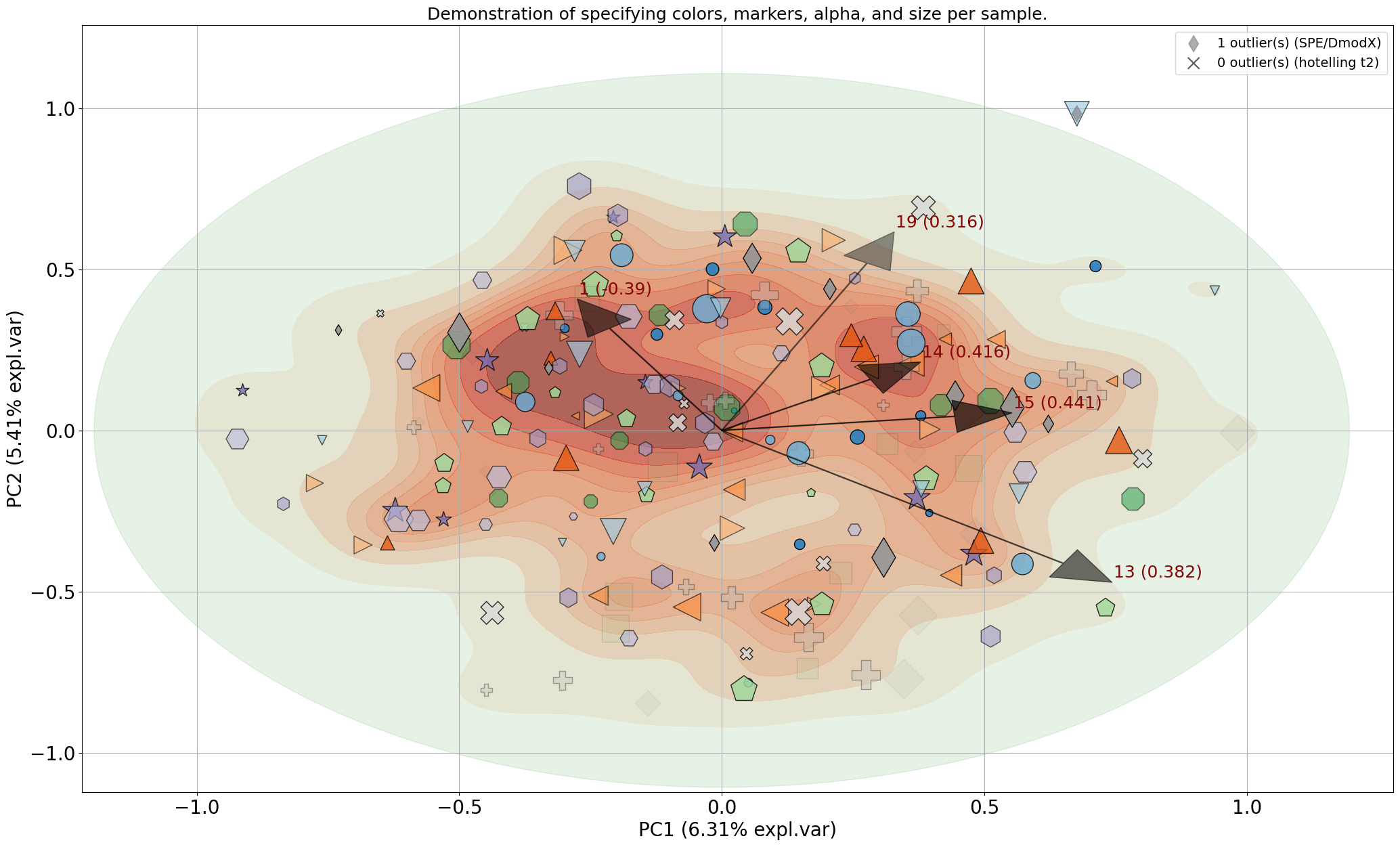
| Alpha Transparency | Normalize Out Principal Components |

|
|
| Extract Feature Importance | |
Make the biplot to visualize the contribution of each feature to the principal components.
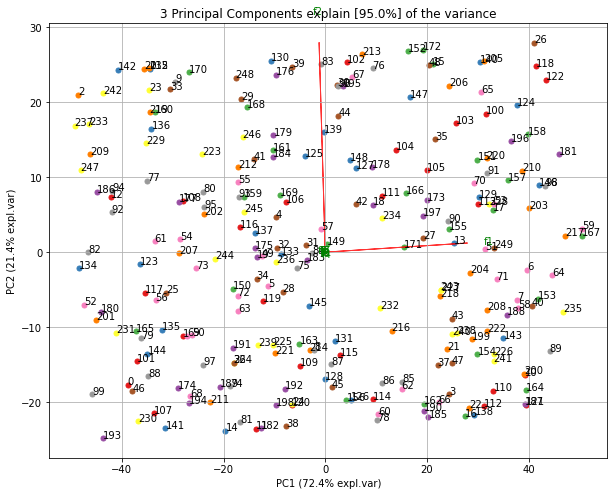
|
|
| Detect Outliers | Show Only Loadings |
Detect outliers using Hotelling's T² and Fisher’s method across top components (PC1–PC5).


|

|
| Select Outliers | Toggle Visibility |
| Select and filter identified outliers for deeper inspection or removal. | Toggle visibility of samples and components to clean up visualizations. |
| Map Unseen Datapoints | |
| Project new data into the transformed PCA space. This enables testing new observations without re-fitting the model. | |
Contributors
Setting up and maintaining PCA has been possible thanks to users and contributors. Thanks to:
Maintainer
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file pca-2.10.1.tar.gz.
File metadata
- Download URL: pca-2.10.1.tar.gz
- Upload date:
- Size: 36.6 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.2.0 CPython/3.12.12
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
8d9b3d9fb0d9fde4a84bf9392ca49a4e9440d4f10432af0dfdf07be20686cf65
|
|
| MD5 |
45493f9d0934d9753463ae1894024f80
|
|
| BLAKE2b-256 |
5b5c7a2329615b54a682a23d650506786afa5ca89da7cc4708a7692d670b1359
|
File details
Details for the file pca-2.10.1-py3-none-any.whl.
File metadata
- Download URL: pca-2.10.1-py3-none-any.whl
- Upload date:
- Size: 34.2 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.2.0 CPython/3.12.12
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
6f0dca39c9327b4fd002a2b758dff485ffcf2611874369085ba703e8cf730624
|
|
| MD5 |
b9bb86ac30fa3ea21c3fa8cb66df23a2
|
|
| BLAKE2b-256 |
17879347c915e49747ea8e98d225ad8bb40ae2f9fdfbc83915579f96d461834f
|





























