Generate modified small-world networks and compare with theoretical predictions.
Project description
Generate and analyze small-world networks according to the revised Watts-Strogatz model where the randomization at β = 1 is truly equal to the Erdős-Rényi network model.
In the Watts-Strogatz model each node rewires its k/2 rightmost edges with probality β. This means that each node has halways minimum degree k/2. Also, at β = 1, each edge has been rewired. Hence the probability of it existing is smaller than k/(N-1), contrary to the ER model.
In the adjusted model, each pair of nodes is connected with a certain connection probability. If the lattice distance between the potentially connected nodes is d(i,j) <= k/2 then they are connected with short-range probability p_S = k / (k + β (N-1-k)), otherwise they’re connected with long-range probability p_L = β * p_S.
Install
pip install smallworld
Beware: smallworld only works with Python 3!
Example
In the following example you can see how to generate and draw according to the model described above.
from smallworld.draw import draw_network
from smallworld import get_smallworld_graph
import matplotlib.pyplot as pl
# define network parameters
N = 21
k_over_2 = 2
betas = [0, 0.025, 1.0]
labels = [ r'$\beta=0$', r'$\beta=0.025$', r'$\beta=1$']
focal_node = 0
fig, ax = pl.subplots(1,3,figsize=(9,3))
# scan beta values
for ib, beta in enumerate(betas):
# generate small-world graphs and draw
G = get_smallworld_graph(N, k_over_2, beta)
draw_network(G,k_over_2,focal_node=focal_node,ax=ax[ib])
ax[ib].set_title(labels[ib],fontsize=11)
# show
pl.subplots_adjust(wspace=0.3)
pl.show()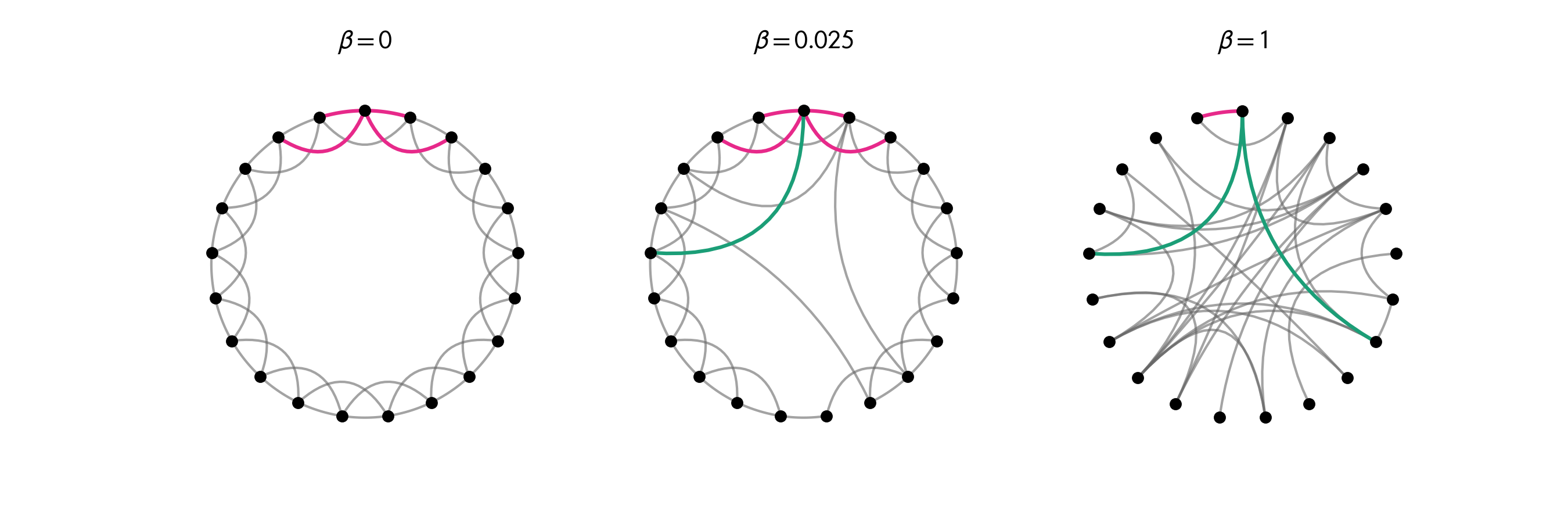
visualization example
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
File details
Details for the file smallworld-0.1.0.tar.gz.
File metadata
- Download URL: smallworld-0.1.0.tar.gz
- Upload date:
- Size: 7.7 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/3.2.0 pkginfo/1.6.1 requests/2.25.0 setuptools/54.2.0 requests-toolbelt/0.9.1 tqdm/4.54.1 CPython/3.8.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
e8950fdb463bcb2f14f9a7a5c357f0d3858520780ba7c3df29792a51d2f14ca5
|
|
| MD5 |
c46e7c57abae926f426feed8cd5593b7
|
|
| BLAKE2b-256 |
b2957aef6a05c85a2e96eeab15d240560021b8f84817d3657534adc23a97299f
|










