Smooth data fitting in N dimensions
Project description
Given experimental data, it is often desirable to produce a function whose values match the data to some degree. This package implements a robust approach to data fitting based on the minimization problem
\|\lambda\Delta f\|^2_{L^2(\Omega)} + \sum_i (f(x_i) - y_i)^2 \to\min
(A similar idea is used in for data smoothing in signal processing; see, e.g., section 8.3 in this document.)
Unlike polynomial regression or Gauss-Newton, smoothfit makes no assumptions about the function other than that it is smooth.
The generality of the approach makes it suitable for function whose domain is multidimensional, too.
Pics or it didn't happen
Runge's example
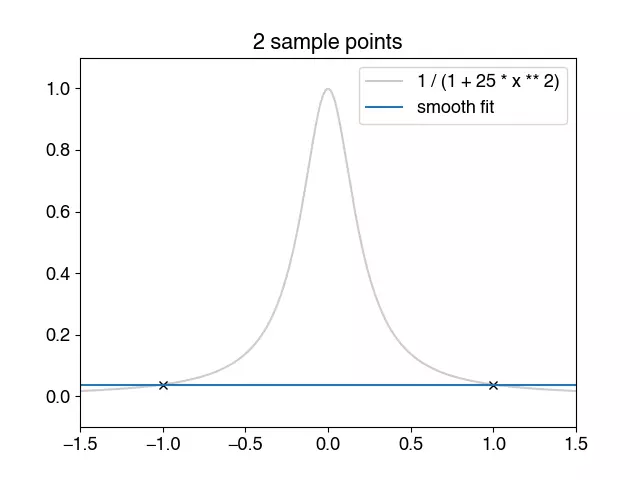
Runge's example function is a tough nut for classical polynomial regression.
If there is no noise in the input data, the parameter lmbda can be chosen quite small
such that all data points are approximated well. Note that there are no oscillations in
the output function u.
import matplotlib.pyplot as plt
import numpy as np
import smoothfit
a = -1.5
b = +1.5
# plot original function
x = np.linspace(a, b, 201)
plt.plot(x, 1 / (1 + 25 * x ** 2), "-", color="0.8", label="1 / (1 + 25 * x**2)")
# sample points
x0 = np.linspace(-1.0, 1.0, 21)
y0 = 1 / (1 + 25 * x0 ** 2)
plt.plot(x0, y0, "xk")
# smoothfit
basis, coeffs = smoothfit.fit1d(x0, y0, a, b, 1000, degree=1, lmbda=1.0e-6)
plt.plot(basis.mesh.p[0], coeffs[basis.nodal_dofs[0]], "-", label="smooth fit")
plt.ylim(-0.1)
plt.grid()
plt.show()
Runge's example with noise
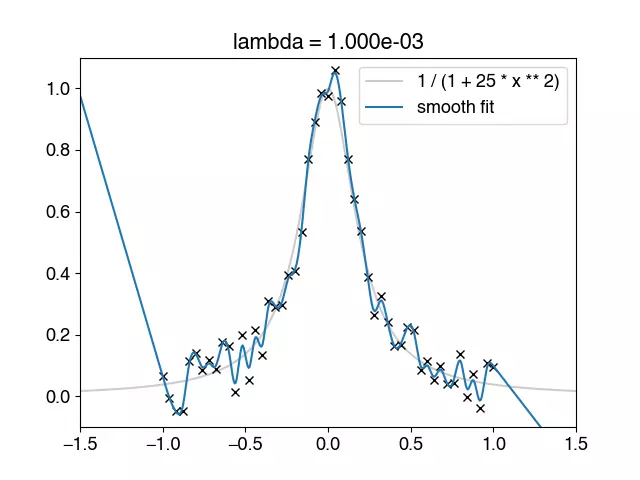
If the data is noisy, lmbda needs to be chosen more carefully. If too small, the
approximation tries to resolve all data points, resulting in many small oscillations.
If it's chosen too large, no details are resolved, not even those of the underlying
data.
import matplotlib.pyplot as plt
import numpy as np
import smoothfit
a = -1.5
b = +1.5
# plot original function
x = np.linspace(a, b, 201)
plt.plot(x, 1 / (1 + 25 * x ** 2), "-", color="0.8", label="1 / (1 + 25 * x**2)")
# 21 sample points
rng = np.random.default_rng(0)
n = 51
x0 = np.linspace(-1.0, 1.0, n)
y0 = 1 / (1 + 25 * x0 ** 2)
y0 += 1.0e-1 * (2 * rng.random(n) - 1)
plt.plot(x0, y0, "xk")
lmbda = 5.0e-2
basis, coeffs = smoothfit.fit1d(x0, y0, a, b, 1000, degree=1, lmbda=lmbda)
plt.plot(basis.mesh.p[0], coeffs[basis.nodal_dofs[0]], "-", label="smooth fit")
plt.grid()
plt.show()
Few samples

import numpy as np
import smoothfit
x0 = np.array([0.038, 0.194, 0.425, 0.626, 1.253, 2.500, 3.740])
y0 = np.array([0.050, 0.127, 0.094, 0.2122, 0.2729, 0.2665, 0.3317])
u = smoothfit.fit1d(x0, y0, 0, 4, 1000, degree=1, lmbda=1.0)
Some noisy example data taken from Wikipedia.
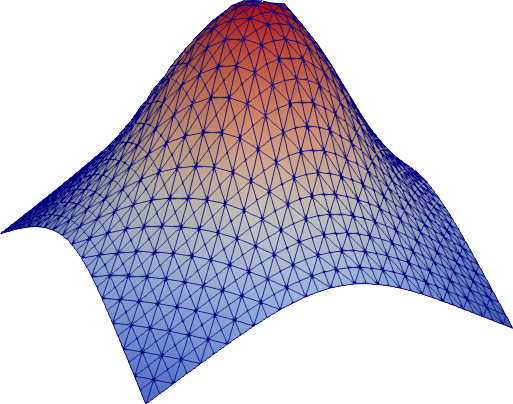
A two-dimensional example
import meshzoo
import numpy as np
import smoothfit
n = 200
rng = np.random.default_rng(123)
x0 = rng.random((n, 2)) - 0.5
y0 = np.cos(np.pi * np.sqrt(x0.T[0] ** 2 + x0.T[1] ** 2))
# create a triangle mesh for the square
points, cells = meshzoo.rectangle_tri(
np.linspace(-1.0, 1.0, 32), np.linspace(-1.0, 1.0, 32)
)
basis, u = smoothfit.fit(x0, y0, points, cells, lmbda=1.0e-4, solver="dense-direct")
# Write the function to a file
basis.mesh.save("out.vtu", point_data={"u": u})
This example approximates a function from R2 to R (without noise in the
samples). Note that the absence of noise the data allows us to pick a rather small
lmbda such that all sample points are approximated well.
Comparison with other approaches
Polynomial fitting/regression
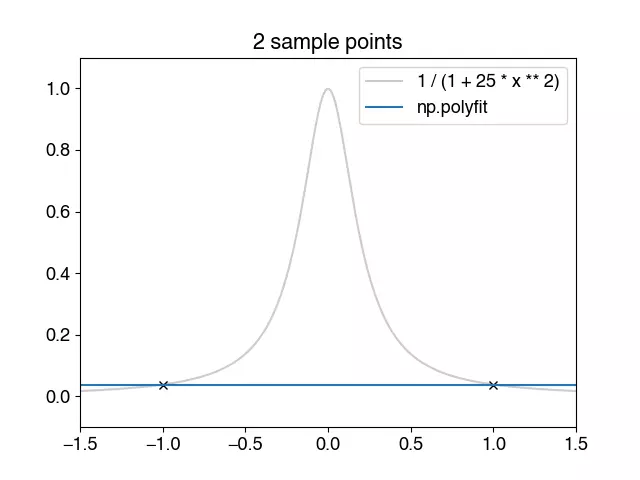
The classical approach to data fitting is polynomial regression. Polynomials are chosen because they are very simple, can be evaluated quickly, and can be made to fit any function very closely.
There are, however, some fundamental problems:
- Your data might not actually fit a polynomial of low degree.
- Runge's phenomenon.
This above plot highlights the problem with oscillations.
Fourier smoothing

One approach to data fitting with smoothing is to create a function with all data points, and simply cut off the high frequencies after Fourier transformation.
This approach is fast, but only works for evenly spaced samples.
For equidistant curve fitting there is nothing else that could compete with the Fourier series. -- Cornelius Lanczos
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.default_rng(0)
# original function
x0 = np.linspace(-1.0, 1.0, 1000)
y0 = 1 / (1 + 25 * x0 ** 2)
plt.plot(x0, y0, color="k", alpha=0.2)
# create sample points
n = 51
x1 = np.linspace(-1.0, 1.0, n) # only works if samples are evenly spaced
y1 = 1 / (1 + 25 * x1 ** 2) + 1.0e-1 * (2 * rng.random(x1.shape[0]) - 1)
plt.plot(x1, y1, "xk")
# Cut off the high frequencies in the transformed space and transform back
X = np.fft.rfft(y1)
X[5:] = 0.0
y2 = np.fft.irfft(X, n)
#
plt.plot(x1, y2, "-", label="5 lowest frequencies")
plt.grid()
plt.show()
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distributions
Built Distribution
File details
Details for the file smoothfit-0.4.1-py3-none-any.whl.
File metadata
- Download URL: smoothfit-0.4.1-py3-none-any.whl
- Upload date:
- Size: 15.8 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/4.0.1 CPython/3.11.2
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
928946c3b80791e28d3a26d0314c4ba20f747b63c94a0470f6fef7ea72873943
|
|
| MD5 |
fe2d2fbe393792b3d5e333968df22ee4
|
|
| BLAKE2b-256 |
f848a0e53c2f8a97f2189ba90596c26b33afbab40479258a9d21e3764aad094e
|
















