Lightweight Covariance Matrix Adaptation Evolution Strategy (CMA-ES) implementation for Python 3.
Project description
cmaes
:whale: Paper is now available on arXiv!
Simple and Practical Python library for CMA-ES. Please refer to the paper [Nomura and Shibata 2024] for detailed information, including the design philosophy and advanced examples.
Installation
Supported Python versions are 3.8 or later.
$ pip install cmaes
Or you can install via conda-forge.
$ conda install -c conda-forge cmaes
Usage
This library provides an "ask-and-tell" style interface. We employ the standard version of CMA-ES [Hansen 2016].
import numpy as np
from cmaes import CMA
def quadratic(x1, x2):
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
if __name__ == "__main__":
optimizer = CMA(mean=np.zeros(2), sigma=1.3)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = quadratic(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
And you can use this library via Optuna [Akiba et al. 2019], an automatic hyperparameter optimization framework. Optuna's built-in CMA-ES sampler which uses this library under the hood is available from v1.3.0 and stabled at v2.0.0. See the documentation or v2.0 release blog for more details.
import optuna
def objective(trial: optuna.Trial):
x1 = trial.suggest_uniform("x1", -4, 4)
x2 = trial.suggest_uniform("x2", -4, 4)
return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2
if __name__ == "__main__":
sampler = optuna.samplers.CmaEsSampler()
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=250)
CMA-ES variants
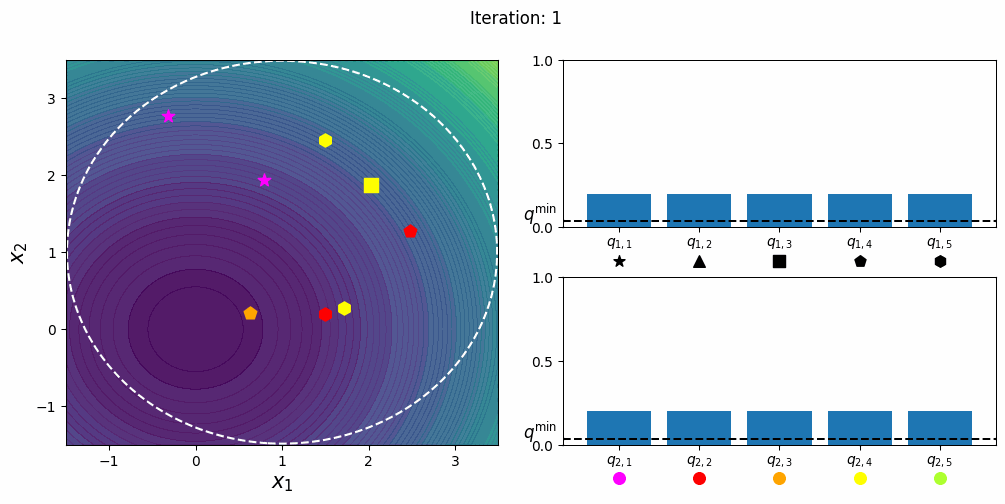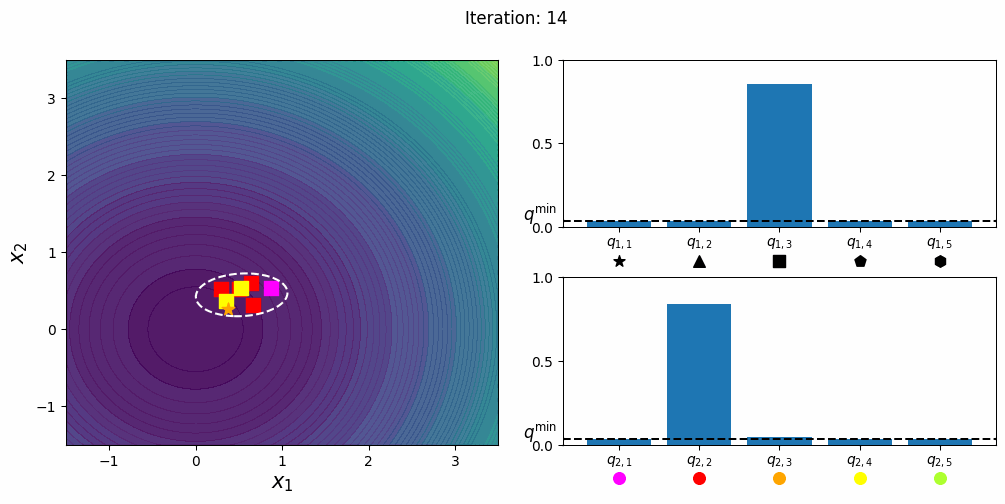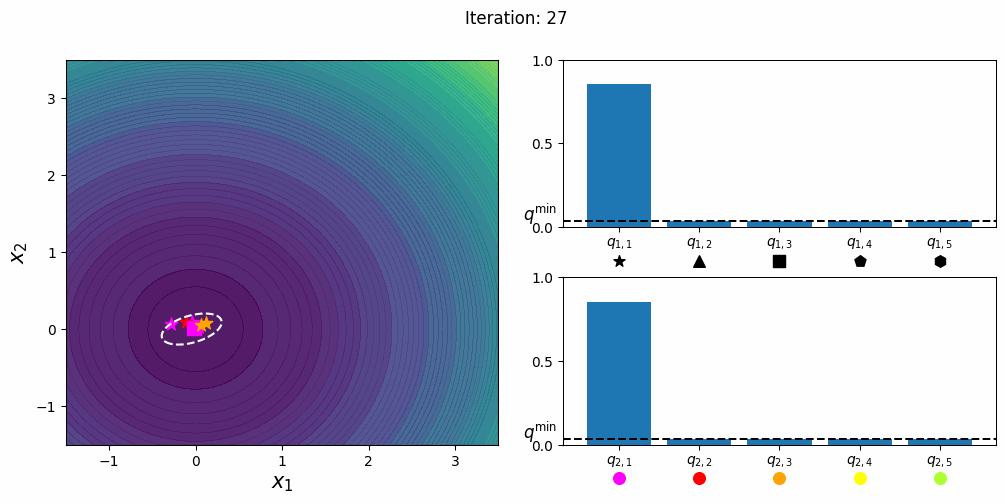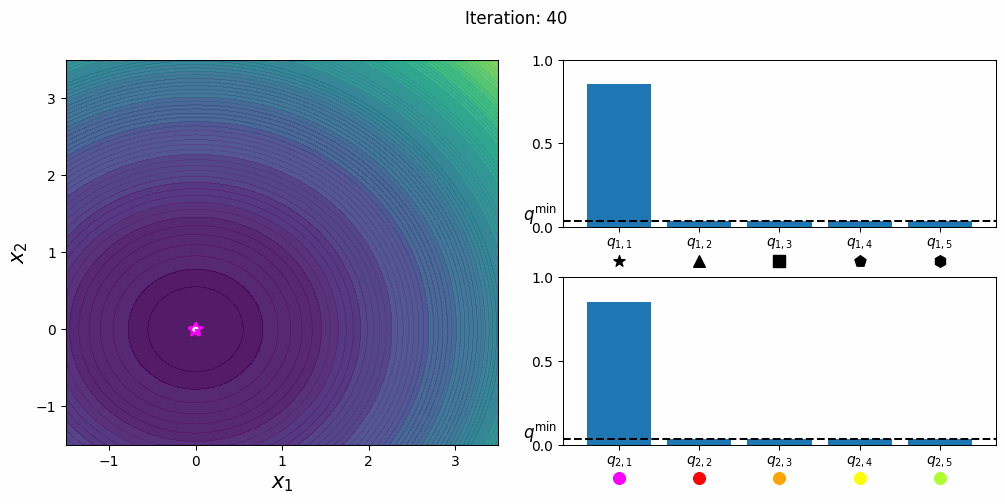
CatCMA with Margin [Hamano et al. 2025]
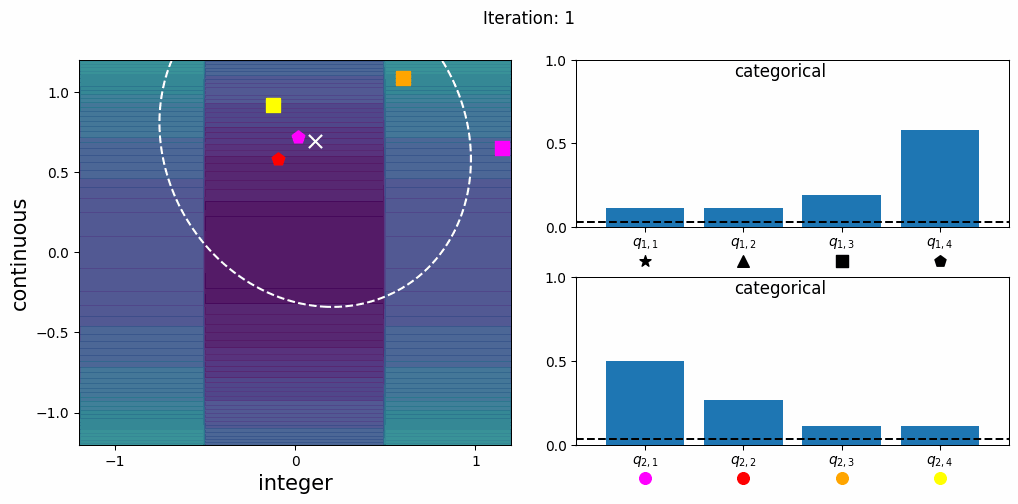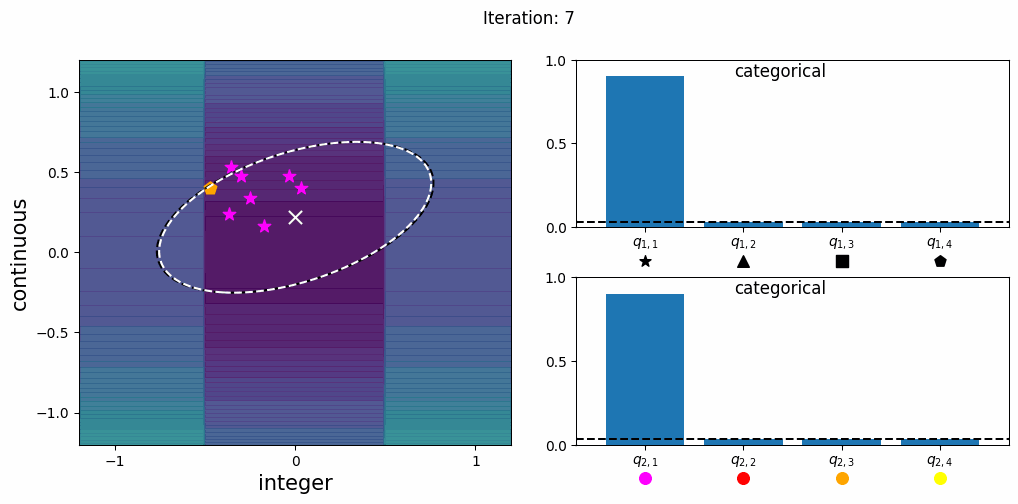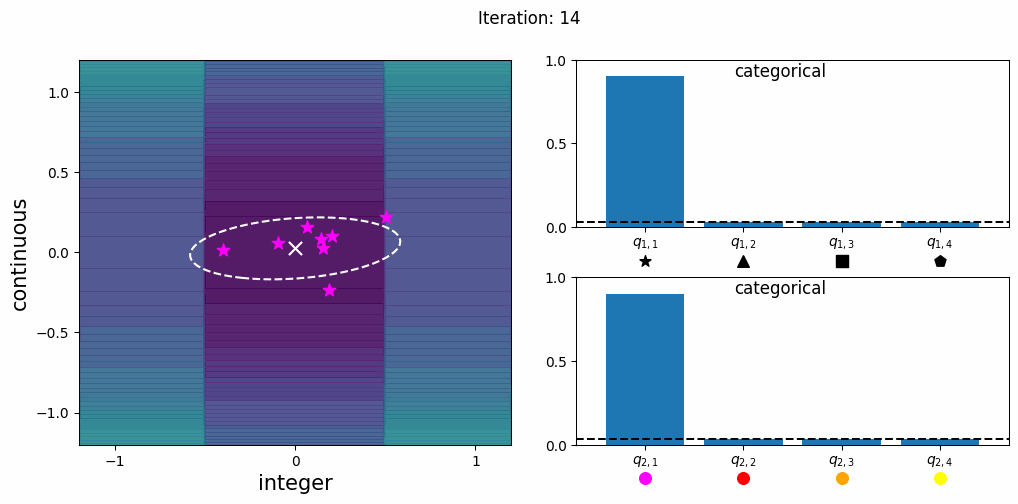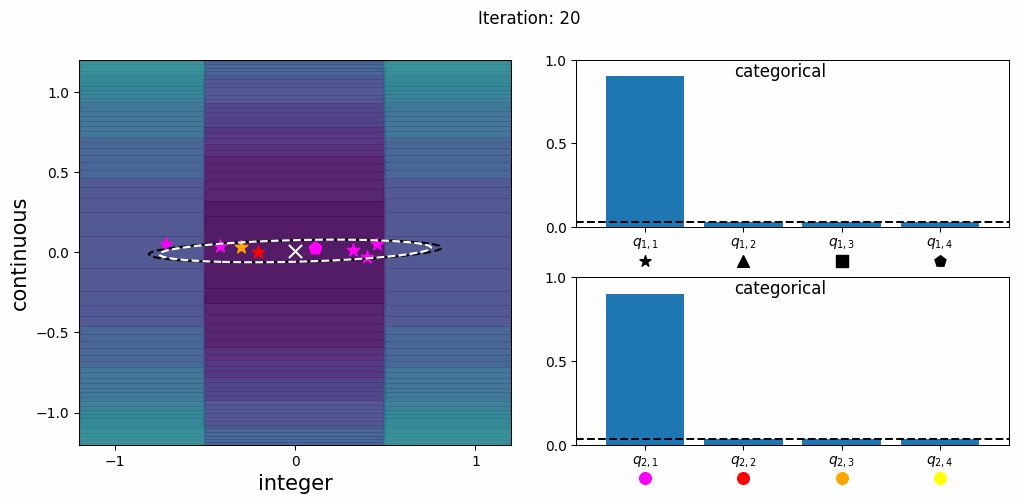
CatCMA with Margin (CatCMAwM) is a method for mixed-variable optimization problems, simultaneously optimizing continuous, integer, and categorical variables. CatCMAwM extends CatCMA by introducing a novel integer handling mechanism, and supports arbitrary combinations of continuous, integer, and categorical variables in a unified framework.
Source code
import numpy as np
from cmaes import CatCMAwM
def SphereIntCOM(x, z, c):
return sum(x * x) + sum(z * z) + len(c) - sum(c[:, 0])
def SphereInt(x, z):
return sum(x * x) + sum(z * z)
def SphereCOM(x, c):
return sum(x * x) + len(c) - sum(c[:, 0])
def f_cont_int_cat():
# [lower_bound, upper_bound] for each continuous variable
X = [[-5, 5], [-5, 5]]
# possible values for each integer variable
Z = [[-1, 0, 1], [-2, -1, 0, 1, 2]]
# number of categories for each categorical variable
C = [3, 3]
optimizer = CatCMAwM(x_space=X, z_space=Z, c_space=C)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
sol = optimizer.ask()
value = SphereIntCOM(sol.x, sol.z, sol.c)
solutions.append((sol, value))
print(f"#{generation} {sol} evaluation: {value}")
optimizer.tell(solutions)
def f_cont_int():
# [lower_bound, upper_bound] for each continuous variable
X = [[-np.inf, np.inf], [-np.inf, np.inf]]
# possible values for each integer variable
Z = [[-2, -1, 0, 1, 2], [-2, -1, 0, 1, 2]]
# initial distribution parameters (Optional)
# If you know a promising solution for X and Z, set init_mean to that value.
init_mean = np.ones(len(X) + len(Z))
init_cov = np.diag(np.ones(len(X) + len(Z)))
init_sigma = 1.0
optimizer = CatCMAwM(
x_space=X, z_space=Z, mean=init_mean, cov=init_cov, sigma=init_sigma
)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
sol = optimizer.ask()
value = SphereInt(sol.x, sol.z)
solutions.append((sol, value))
print(f"#{generation} {sol} evaluation: {value}")
optimizer.tell(solutions)
def f_cont_cat():
# [lower_bound, upper_bound] for each continuous variable
X = [[-5, 5], [-5, 5]]
# number of categories for each categorical variable
C = [3, 5]
# initial distribution parameters (Optional)
init_cat_param = np.array(
[
[0.5, 0.3, 0.2, 0.0, 0.0], # zero-padded at the end
[0.2, 0.2, 0.2, 0.2, 0.2], # each row must sum to 1
]
)
optimizer = CatCMAwM(x_space=X, c_space=C, cat_param=init_cat_param)
for generation in range(50):
solutions = []
for _ in range(optimizer.population_size):
sol = optimizer.ask()
value = SphereCOM(sol.x, sol.c)
solutions.append((sol, value))
print(f"#{generation} {sol} evaluation: {value}")
optimizer.tell(solutions)
if __name__ == "__main__":
f_cont_int_cat()
# f_cont_int()
# f_cont_cat()
The full source code is available here.
We recommend using CatCMAwM for continuous+integer and continuous+categorical settings. In particular, [Hamano et al. 2025] shows that CatCMAwM outperforms CMA-ES with Margin in mixed-integer scenarios. Therefore, we suggest CatCMAwM in place of CMA-ES with Margin or CatCMA.
CatCMA [Hamano et al. 2024a]
CatCMA is a method for mixed-category optimization problems, which is the problem of simultaneously optimizing continuous and categorical variables. CatCMA employs the joint probability distribution of multivariate Gaussian and categorical distributions as the search distribution.
Source code
import numpy as np
from cmaes import CatCMA
def sphere_com(x, c):
dim_co = len(x)
dim_ca = len(c)
if dim_co < 2:
raise ValueError("dimension must be greater one")
sphere = sum(x * x)
com = dim_ca - sum(c[:, 0])
return sphere + com
def rosenbrock_clo(x, c):
dim_co = len(x)
dim_ca = len(c)
if dim_co < 2:
raise ValueError("dimension must be greater one")
rosenbrock = sum(100 * (x[:-1] ** 2 - x[1:]) ** 2 + (x[:-1] - 1) ** 2)
clo = dim_ca - (c[:, 0].argmin() + c[:, 0].prod() * dim_ca)
return rosenbrock + clo
def mc_proximity(x, c, cat_num):
dim_co = len(x)
dim_ca = len(c)
if dim_co < 2:
raise ValueError("dimension must be greater one")
if dim_co != dim_ca:
raise ValueError(
"number of dimensions of continuous and categorical variables "
"must be equal in mc_proximity"
)
c_index = np.argmax(c, axis=1) / cat_num
return sum((x - c_index) ** 2) + sum(c_index)
if __name__ == "__main__":
cont_dim = 5
cat_dim = 5
cat_num = np.array([3, 4, 5, 5, 5])
# cat_num = 3 * np.ones(cat_dim, dtype=np.int64)
optimizer = CatCMA(mean=3.0 * np.ones(cont_dim), sigma=1.0, cat_num=cat_num)
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x, c = optimizer.ask()
value = mc_proximity(x, c, cat_num)
if generation % 10 == 0:
print(f"#{generation} {value}")
solutions.append(((x, c), value))
optimizer.tell(solutions)
if optimizer.should_stop():
break
The full source code is available here.
Safe CMA [Uchida et al. 2024a]
Safe CMA-ES is a variant of CMA-ES for safe optimization. Safe optimization is formulated as a special type of constrained optimization problem aiming to solve the optimization problem with fewer evaluations of the solutions whose safety function values exceed the safety thresholds. The safe CMA-ES requires safe seeds that do not violate the safety constraints. Note that the safe CMA-ES is designed for noiseless safe optimization. This module needs torch and gpytorch.
Source code
import numpy as np
from cmaes.safe_cma import SafeCMA
# objective function
def quadratic(x):
coef = 1000 ** (np.arange(dim) / float(dim - 1))
return np.sum((x * coef) ** 2)
# safety function
def safe_function(x):
return x[0]
"""
example with a single safety function
"""
if __name__ == "__main__":
# number of dimensions
dim = 5
# safe seeds
safe_seeds_num = 10
safe_seeds = (np.random.rand(safe_seeds_num, dim) * 2 - 1) * 5
safe_seeds[:,0] = - np.abs(safe_seeds[:,0])
# evaluation of safe seeds (with a single safety function)
seeds_evals = np.array([ quadratic(x) for x in safe_seeds ])
seeds_safe_evals = np.stack([ [safe_function(x)] for x in safe_seeds ])
safety_threshold = np.array([0])
# optimizer (safe CMA-ES)
optimizer = SafeCMA(
sigma=1.,
safety_threshold=safety_threshold,
safe_seeds=safe_seeds,
seeds_evals=seeds_evals,
seeds_safe_evals=seeds_safe_evals,
)
unsafe_eval_counts = 0
best_eval = np.inf
for generation in range(400):
solutions = []
for _ in range(optimizer.population_size):
# Ask a parameter
x = optimizer.ask()
value = quadratic(x)
safe_value = np.array([safe_function(x)])
# save best eval
best_eval = np.min((best_eval, value))
unsafe_eval_counts += (safe_value > safety_threshold)
solutions.append((x, value, safe_value))
# Tell evaluation values.
optimizer.tell(solutions)
print(f"#{generation} ({best_eval} {unsafe_eval_counts})")
if optimizer.should_stop():
break
The full source code is available here.
Maximum a Posteriori CMA-ES [Hamano et al. 2024b]
MAP-CMA is a method that is introduced to interpret the rank-one update in the CMA-ES from the perspective of the natural gradient. The rank-one update derived from the natural gradient perspective is extensible, and an additional term, called momentum update, appears in the update of the mean vector. The performance of MAP-CMA is not significantly different from that of CMA-ES, as the primary motivation for MAP-CMA comes from the theoretical understanding of CMA-ES.
Source code
import numpy as np
from cmaes import MAPCMA
def rosenbrock(x):
dim = len(x)
if dim < 2:
raise ValueError("dimension must be greater one")
return sum(100 * (x[:-1] ** 2 - x[1:]) ** 2 + (x[:-1] - 1) ** 2)
if __name__ == "__main__":
dim = 20
optimizer = MAPCMA(mean=np.zeros(dim), sigma=0.5, momentum_r=dim)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = rosenbrock(x)
evals += 1
solutions.append((x, value))
if evals % 1000 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
The full source code is available here.
CMA-ES-SoP [Uchida et al. 2024b]
CMA-ES on sets of points (CMA-ES-SoP) is a variant of CMA-ES for optimization on sets of points. In the optimization on sets of points, the search space consists of several disjoint subspaces containing multiple possible points where the objective function value can be computed. In the mixed-variable cases, some subspaces are continuous spaces. Note that the discrete subspaces with more than five dimensions require computational cost for the construction of the Voronoi diagrams.
Source code
import numpy as np
from cmaes.cma_sop import CMASoP
# numbers of dimensions in each subspace
subspace_dim_list = [2, 3, 5]
cont_dim = 10
# numbers of points in each subspace
point_num_list = [10, 20, 40]
# number of total dimensions
dim = int(np.sum(subspace_dim_list) + cont_dim)
# objective function
def quadratic(x):
coef = 1000 ** (np.arange(dim) / float(dim - 1))
return np.sum((coef * x) ** 2)
# sets_of_points (on [-5, 5])
discrete_subspace_num = len(subspace_dim_list)
sets_of_points = [(
2 * np.random.rand(point_num_list[i], subspace_dim_list[i]) - 1) * 5
for i in range(discrete_subspace_num)]
# add the optimal solution (for benchmark function)
for i in range(discrete_subspace_num):
sets_of_points[i][-1] = np.zeros(subspace_dim_list[i])
np.random.shuffle(sets_of_points[i])
# optimizer (CMA-ES-SoP)
optimizer = CMASoP(
sets_of_points=sets_of_points,
mean=np.random.rand(dim) * 4 + 1,
sigma=2.0,
)
best_eval = np.inf
eval_count = 0
for generation in range(400):
solutions = []
for _ in range(optimizer.population_size):
# Ask a parameter
x, enc_x = optimizer.ask()
value = quadratic(enc_x)
# save best eval
best_eval = np.min((best_eval, value))
eval_count += 1
solutions.append((x, value))
# Tell evaluation values.
optimizer.tell(solutions)
print(f"#{generation} ({best_eval} {eval_count})")
if best_eval < 1e-4 or optimizer.should_stop():
break
The full source code is available here.
Learning Rate Adaptation CMA-ES [Nomura et al. 2023]
The performance of the CMA-ES can deteriorate when faced with difficult problems such as multimodal or noisy ones, if its hyperparameter values are not properly configured. The Learning Rate Adaptation CMA-ES (LRA-CMA) effectively addresses this issue by autonomously adjusting the learning rate. Consequently, LRA-CMA eliminates the need for expensive hyperparameter tuning.
LRA-CMA can be used by simply adding lr_adapt=True to the initialization of CMA().
Source code
import numpy as np
from cmaes import CMA
def rastrigin(x):
dim = len(x)
return 10 * dim + sum(x**2 - 10 * np.cos(2 * np.pi * x))
if __name__ == "__main__":
dim = 40
optimizer = CMA(mean=3*np.ones(dim), sigma=2.0, lr_adapt=True)
for generation in range(50000):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = rastrigin(x)
if generation % 500 == 0:
print(f"#{generation} {value}")
solutions.append((x, value))
optimizer.tell(solutions)
if optimizer.should_stop():
break
The full source code is available here.
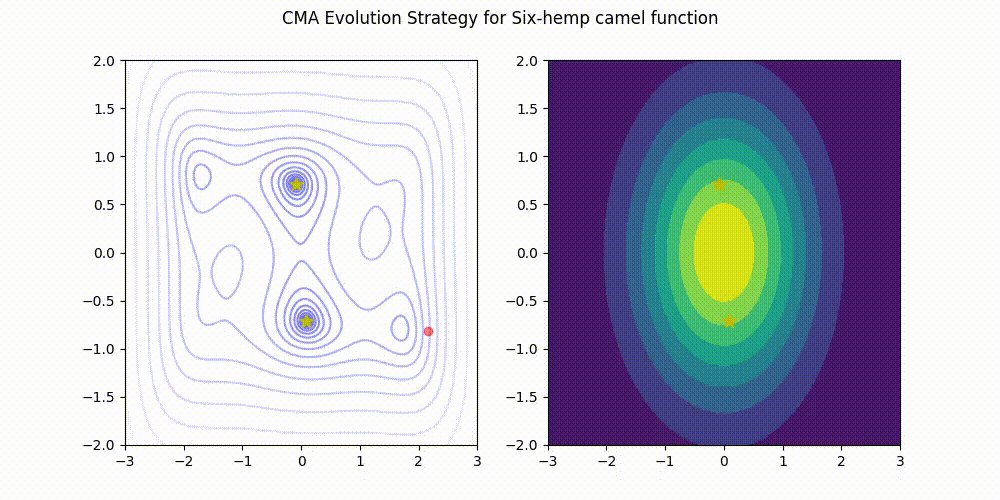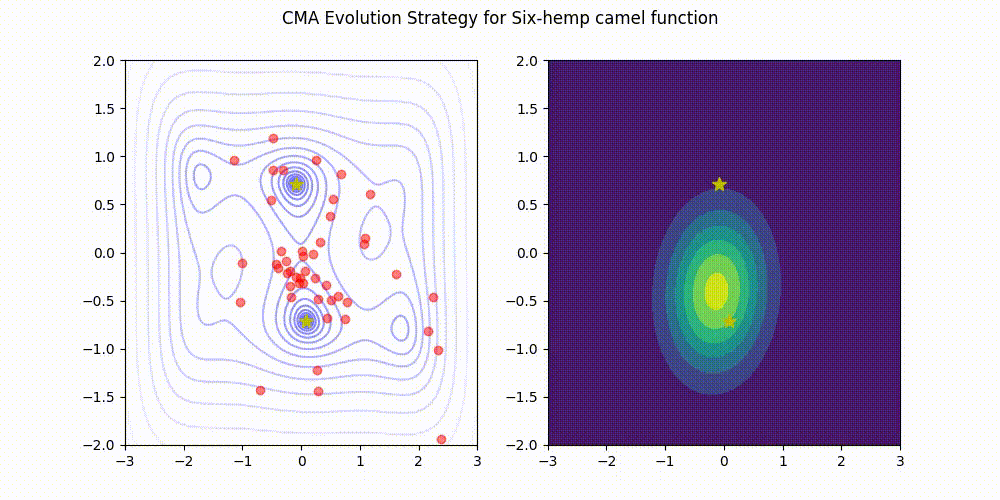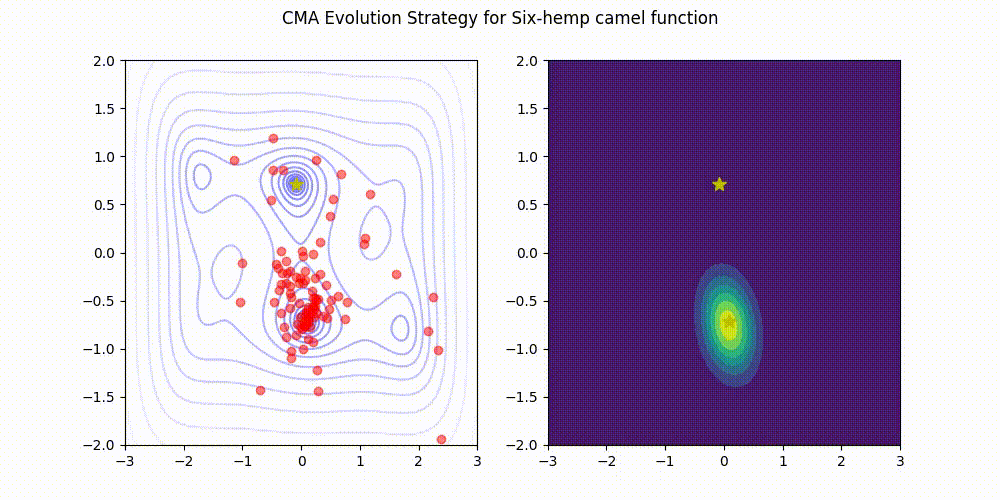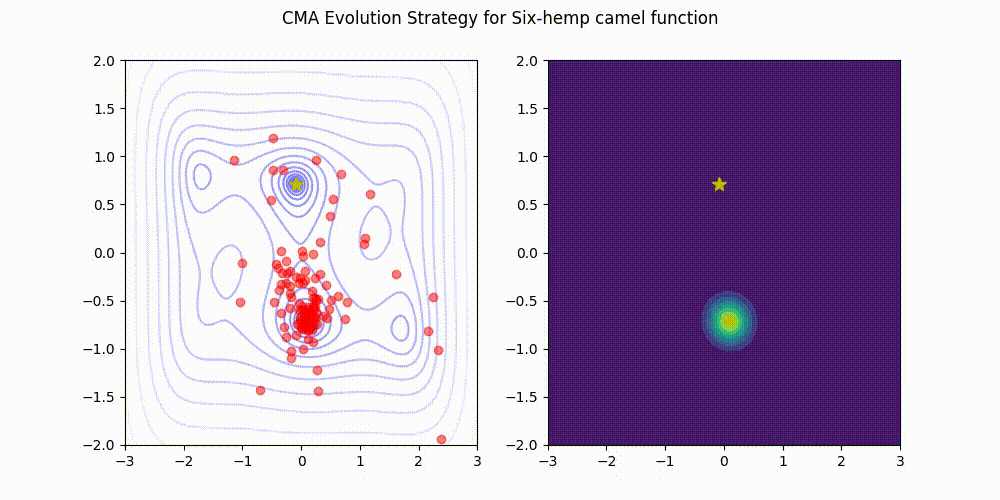
CMA-ES with Margin [Hamano et al. 2022]
CMA-ES with Margin (CMAwM) introduces a lower bound on the marginal probability for each discrete dimension, ensuring that samples avoid being fixed to a single point. This method can be applied to mixed spaces consisting of continuous (such as float) and discrete elements (including integer and binary types).
| CMA | CMAwM |
|---|---|
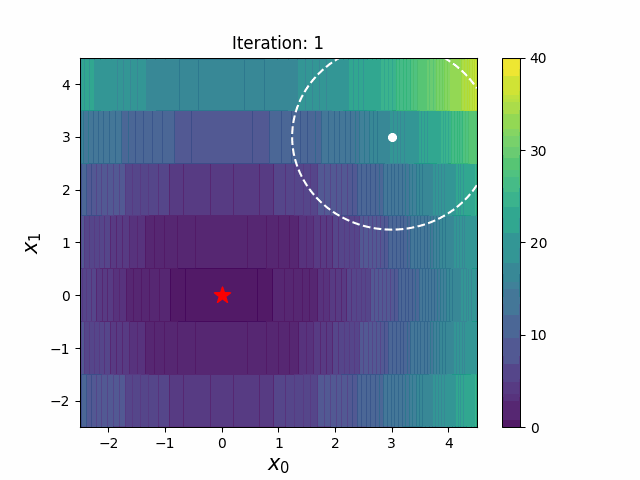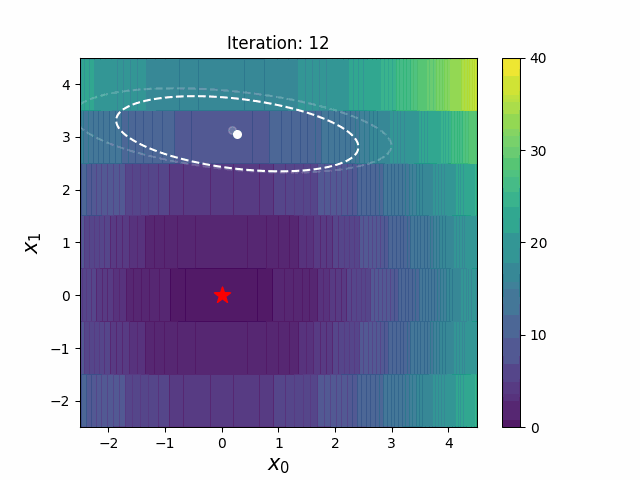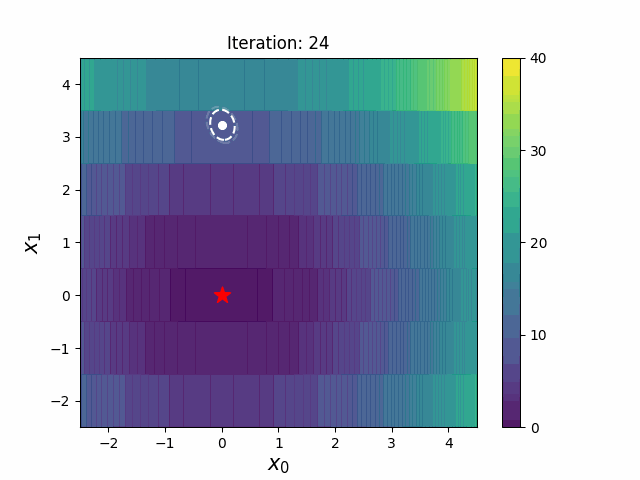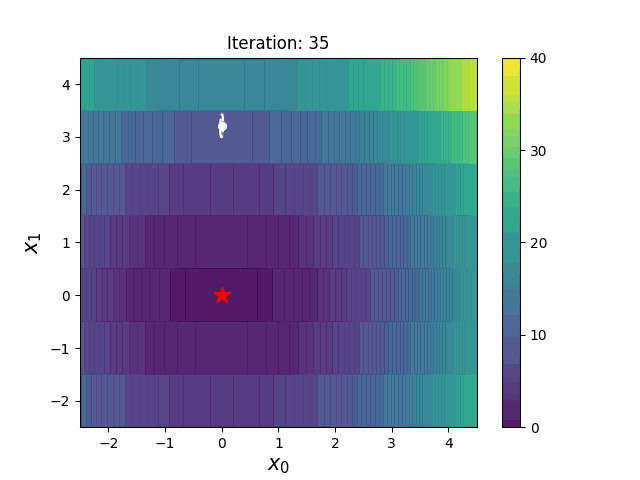 |
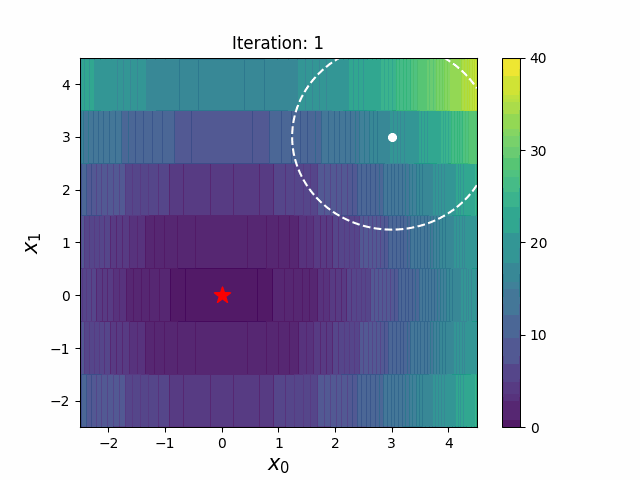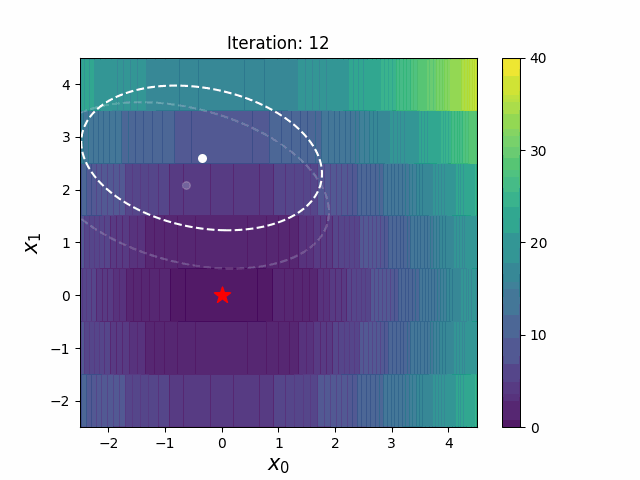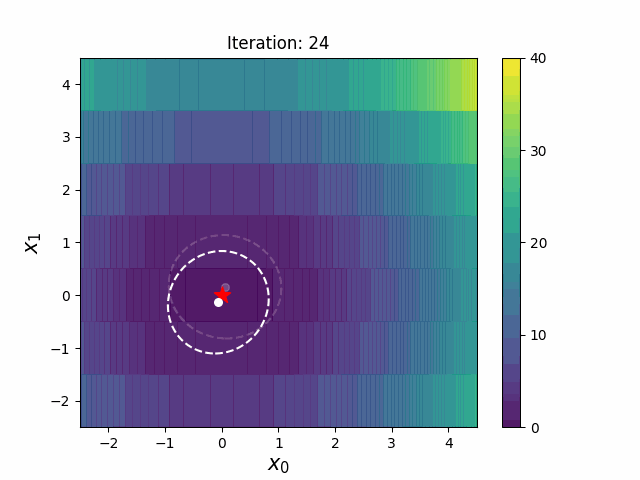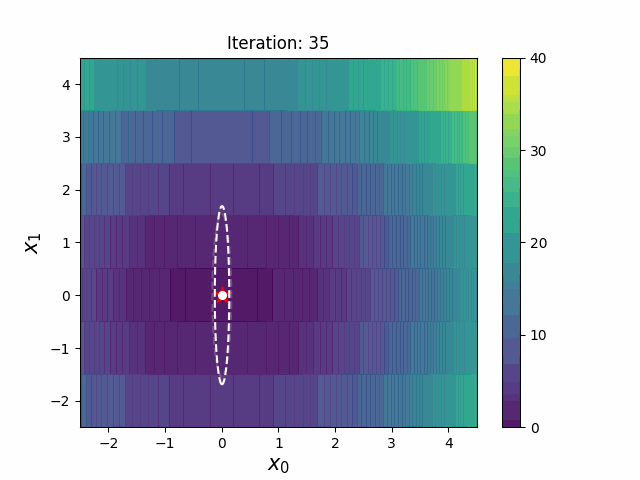 |
The above figures are taken from EvoConJP/CMA-ES_with_Margin.
Source code
import numpy as np
from cmaes import CMAwM
def ellipsoid_onemax(x, n_zdim):
n = len(x)
n_rdim = n - n_zdim
r = 10
if len(x) < 2:
raise ValueError("dimension must be greater one")
ellipsoid = sum([(1000 ** (i / (n_rdim - 1)) * x[i]) ** 2 for i in range(n_rdim)])
onemax = n_zdim - (0.0 < x[(n - n_zdim) :]).sum()
return ellipsoid + r * onemax
def main():
binary_dim, continuous_dim = 10, 10
dim = binary_dim + continuous_dim
bounds = np.concatenate(
[
np.tile([-np.inf, np.inf], (continuous_dim, 1)),
np.tile([0, 1], (binary_dim, 1)),
]
)
steps = np.concatenate([np.zeros(continuous_dim), np.ones(binary_dim)])
optimizer = CMAwM(mean=np.zeros(dim), sigma=2.0, bounds=bounds, steps=steps)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = ellipsoid_onemax(x_for_eval, binary_dim)
evals += 1
solutions.append((x_for_tell, value))
if evals % 300 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
if __name__ == "__main__":
main()
Source code is also available here.
Warm Starting CMA-ES [Nomura et al. 2021]
Warm Starting CMA-ES (WS-CMA) is a method that transfers prior knowledge from similar tasks through the initialization of the CMA-ES. This is useful especially when the evaluation budget is limited (e.g., hyperparameter optimization of machine learning algorithms).
Source code
import numpy as np
from cmaes import CMA, get_warm_start_mgd
def source_task(x1: float, x2: float) -> float:
b = 0.4
return (x1 - b) ** 2 + (x2 - b) ** 2
def target_task(x1: float, x2: float) -> float:
b = 0.6
return (x1 - b) ** 2 + (x2 - b) ** 2
if __name__ == "__main__":
# Generate solutions from a source task
source_solutions = []
for _ in range(1000):
x = np.random.random(2)
value = source_task(x[0], x[1])
source_solutions.append((x, value))
# Estimate a promising distribution of the source task,
# then generate parameters of the multivariate gaussian distribution.
ws_mean, ws_sigma, ws_cov = get_warm_start_mgd(
source_solutions, gamma=0.1, alpha=0.1
)
optimizer = CMA(mean=ws_mean, sigma=ws_sigma, cov=ws_cov)
# Run WS-CMA-ES
print(" g f(x1,x2) x1 x2 ")
print("=== ========== ====== ======")
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = target_task(x[0], x[1])
solutions.append((x, value))
print(
f"{optimizer.generation:3d} {value:10.5f}"
f" {x[0]:6.2f} {x[1]:6.2f}"
)
optimizer.tell(solutions)
if optimizer.should_stop():
break
The full source code is available here.
Separable CMA-ES [Ros and Hansen 2008]
Sep-CMA-ES is an algorithm that limits the covariance matrix to a diagonal form. This reduction in the number of parameters enhances scalability, making Sep-CMA-ES well-suited for high-dimensional optimization tasks. Additionally, the learning rate for the covariance matrix is increased, leading to superior performance over the (full-covariance) CMA-ES on separable functions.
Source code
import numpy as np
from cmaes import SepCMA
def ellipsoid(x):
n = len(x)
if len(x) < 2:
raise ValueError("dimension must be greater one")
return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])
if __name__ == "__main__":
dim = 40
optimizer = SepCMA(mean=3 * np.ones(dim), sigma=2.0)
print(" evals f(x)")
print("====== ==========")
evals = 0
while True:
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ellipsoid(x)
evals += 1
solutions.append((x, value))
if evals % 3000 == 0:
print(f"{evals:5d} {value:10.5f}")
optimizer.tell(solutions)
if optimizer.should_stop():
break
Full source code is available here.
IPOP-CMA-ES [Auger and Hansen 2005]
IPOP-CMA-ES is a method that involves restarting the CMA-ES with an incrementally increasing population size, as described below.
Source code
import math
import numpy as np
from cmaes import CMA
def ackley(x1, x2):
# https://www.sfu.ca/~ssurjano/ackley.html
return (
-20 * math.exp(-0.2 * math.sqrt(0.5 * (x1 ** 2 + x2 ** 2)))
- math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
+ math.e + 20
)
if __name__ == "__main__":
bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
sigma = 32.768 * 2 / 5 # 1/5 of the domain width
optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)
for generation in range(200):
solutions = []
for _ in range(optimizer.population_size):
x = optimizer.ask()
value = ackley(x[0], x[1])
solutions.append((x, value))
print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
optimizer.tell(solutions)
if optimizer.should_stop():
# popsize multiplied by 2 (or 3) before each restart.
popsize = optimizer.population_size * 2
mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
optimizer = CMA(mean=mean, sigma=sigma, population_size=popsize)
print(f"Restart CMA-ES with popsize={popsize}")
Full source code is available here.
Citation
If you use our library in your work, please cite our paper:
Masahiro Nomura, Masashi Shibata.
cmaes : A Simple yet Practical Python Library for CMA-ES
https://arxiv.org/abs/2402.01373
Bibtex:
@article{nomura2024cmaes,
title={cmaes : A Simple yet Practical Python Library for CMA-ES},
author={Nomura, Masahiro and Shibata, Masashi},
journal={arXiv preprint arXiv:2402.01373},
year={2024}
}
Links
Projects using cmaes:
- Optuna : A hyperparameter optimization framework that supports CMA-ES using this library under the hood.
- Kubeflow/Katib : Kubernetes-based system for hyperparameter tuning and neural architecture search
- (If you are using
cmaesin your project and would like it to be listed here, please submit a GitHub issue.)
Other libraries:
We have great respect for all libraries involved in CMA-ES.
- pycma : Most renowned CMA-ES implementation, created and maintained by Nikolaus Hansen.
- pymoo : A library for multi-objective optimization in Python.
- evojax : evojax offers a JAX-port of this library.
- evosax : evosax provides a JAX-based implementation of CMA-ES and sep-CMA-ES, inspired by this library.
References:
- [Akiba et al. 2019] T. Akiba, S. Sano, T. Yanase, T. Ohta, M. Koyama, Optuna: A Next-generation Hyperparameter Optimization Framework, KDD, 2019.
- [Auger and Hansen 2005] A. Auger, N. Hansen, A Restart CMA Evolution Strategy with Increasing Population Size, CEC, 2005.
- [Hamano et al. 2022] R. Hamano, S. Saito, M. Nomura, S. Shirakawa, CMA-ES with Margin: Lower-Bounding Marginal Probability for Mixed-Integer Black-Box Optimization, GECCO, 2022.
- [Hamano et al. 2024a] R. Hamano, S. Saito, M. Nomura, K. Uchida, S. Shirakawa, CatCMA : Stochastic Optimization for Mixed-Category Problems, GECCO, 2024.
- [Hamano et al. 2025] R. Hamano, M. Nomura, S. Saito, K. Uchida, S. Shirakawa, CatCMA with Margin: Stochastic Optimization for Continuous, Integer, and Categorical Variables, GECCO, 2025.
- [Hamano et al. 2024b] R. Hamano, S. Shirakawa, M. Nomura, Natural Gradient Interpretation of Rank-One Update in CMA-ES, PPSN, 2024.
- [Hansen 2016] N. Hansen, The CMA Evolution Strategy: A Tutorial. arXiv:1604.00772, 2016.
- [Nomura et al. 2021] M. Nomura, S. Watanabe, Y. Akimoto, Y. Ozaki, M. Onishi, Warm Starting CMA-ES for Hyperparameter Optimization, AAAI, 2021.
- [Nomura et al. 2023] M. Nomura, Y. Akimoto, I. Ono, CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?, GECCO, 2023.
- [Nomura and Shibata 2024] M. Nomura, M. Shibata, cmaes : A Simple yet Practical Python Library for CMA-ES, arXiv:2402.01373, 2024.
- [Ros and Hansen 2008] R. Ros, N. Hansen, A Simple Modification in CMA-ES Achieving Linear Time and Space Complexity, PPSN, 2008.
- [Uchida et al. 2024a] K. Uchida, R. Hamano, M. Nomura, S. Saito, S. Shirakawa, CMA-ES for Safe Optimization, GECCO, 2024.
- [Uchida et al. 2024b] K. Uchida, R. Hamano, M. Nomura, S. Saito, S. Shirakawa, CMA-ES for Discrete and Mixed-Variable Optimization on Sets of Points, PPSN, 2024.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
Filter files by name, interpreter, ABI, and platform.
If you're not sure about the file name format, learn more about wheel file names.
Copy a direct link to the current filters
File details
Details for the file cmaes-0.12.0.tar.gz.
File metadata
- Download URL: cmaes-0.12.0.tar.gz
- Upload date:
- Size: 52.8 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
6aab41eee2f38bf917560a7e7d1ba0060632cd44cdf7ac2a10704da994624182
|
|
| MD5 |
4d10af15119c1ded69227bc4a50e5558
|
|
| BLAKE2b-256 |
5b4b9633e72dcd9ac28ab72c661feeb7ece5d01b55e7c9b0ef3331fb102e1506
|
File details
Details for the file cmaes-0.12.0-py3-none-any.whl.
File metadata
- Download URL: cmaes-0.12.0-py3-none-any.whl
- Upload date:
- Size: 64.5 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: twine/6.1.0 CPython/3.12.9
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 |
d0e3e50ce28a36294bffa16a5626c15d23155824cf6b0a373db30dbbea9b2256
|
|
| MD5 |
38f1601d0480c07639811990f6437d56
|
|
| BLAKE2b-256 |
3357f78b7ed51b3536cc80b4322db2cbbb9d1f409736b852eef0493d9fd8474d
|