Quadratic programming solvers in Python with a unified API.
Project description
QP Solvers for Python
Unified interface to convex Quadratic Programming (QP) solvers available in Python.
Installation
Using PyPI
pip install qpsolvers
Using 
conda install qpsolvers -c conda-forge
Check out the documentation for Windows instructions.
Usage
The library provides a one-stop shop solve_qp function with a solver keyword argument to select the backend solver. It solves convex quadratic programs in standard form:
$$ \begin{split} \begin{array}{ll} \underset{x}{\mbox{minimize}} & \frac{1}{2} x^T P x + q^T x \ \mbox{subject to} & G x \leq h \ & A x = b \ & lb \leq x \leq ub \end{array} \end{split} $$
Vector inequalities apply coordinate by coordinate. The function returns the solution $x^*$ found by the solver, or None in case of failure/unfeasible problem. All solvers require the problem to be convex, meaning the matrix $P$ should be positive semi-definite. Some solvers further require the problem to be strictly convex, meaning $P$ should be positive definite.
Dual multipliers: alternatively, the solve_problem function returns a more complete solution object containing both the primal solution and its corresponding dual multipliers.
Example
To solve a quadratic program, build the matrices that define it and call the solve_qp function:
import numpy as np
from qpsolvers import solve_qp
M = np.array([[1.0, 2.0, 0.0], [-8.0, 3.0, 2.0], [0.0, 1.0, 1.0]])
P = M.T @ M # this is a positive definite matrix
q = np.array([3.0, 2.0, 3.0]) @ M
G = np.array([[1.0, 2.0, 1.0], [2.0, 0.0, 1.0], [-1.0, 2.0, -1.0]])
h = np.array([3.0, 2.0, -2.0])
A = np.array([1.0, 1.0, 1.0])
b = np.array([1.0])
x = solve_qp(P, q, G, h, A, b, solver="proxqp")
print(f"QP solution: x = {x}")
This example outputs the solution [0.30769231, -0.69230769, 1.38461538]. It is also possible to get dual multipliers at the solution, as shown in this example.
Solvers
| Solver | Keyword | Algorithm | API | License | Warm-start |
|---|---|---|---|---|---|
| Clarabel | clarabel |
Interior point | Dense | Apache-2.0 | ✖️ |
| CVXOPT | cvxopt |
Interior point | Dense | GPL-3.0 | ✔️ |
| ECOS | ecos |
Interior point | Sparse | GPL-3.0 | ✖️ |
| Gurobi | gurobi |
Interior point | Sparse | Commercial | ✖️ |
| HiGHS | highs |
Active set | Sparse | MIT | ✖️ |
| MOSEK | mosek |
Interior point | Sparse | Commercial | ✔️ |
| OSQP | osqp |
Augmented Lagrangian | Sparse | Apache-2.0 | ✔️ |
| ProxQP | proxqp |
Augmented Lagrangian | Dense & Sparse | BSD-2-Clause | ✔️ |
| qpOASES | qpoases |
Active set | Dense | LGPL-2.1 | ➖ |
| qpSWIFT | qpswift |
Interior point | Sparse | GPL-3.0 | ✖️ |
| quadprog | quadprog |
Active set | Dense | GPL-2.0 | ✖️ |
| SCS | scs |
Augmented Lagrangian | Sparse | MIT | ✔️ |
Matrix arguments are NumPy arrays for dense solvers and SciPy Compressed Sparse Column (CSC) matrices for sparse ones.
Frequently Asked Questions
- Can I print the list of solvers available on my machine?
- Absolutely:
print(qpsolvers.available_solvers)
- Absolutely:
- Is it possible to solve a least squares rather than a quadratic program?
- Yes, there is also a
solve_lsfunction.
- Yes, there is also a
- I have a squared norm in my cost function, how can I apply a QP solver to my problem?
- You can cast squared norms to QP matrices and feed the result to
solve_qp.
- You can cast squared norms to QP matrices and feed the result to
- I have a non-convex quadratic program. Is there a solver I can use?
- Unfortunately most available QP solvers are designed for convex problems (i.e. problems for which
Pis positive semidefinite). That's in a way expected, as solving non-convex QP problems is NP hard. - CPLEX has methods for solving non-convex quadratic problems to either local or global optimality. Notice that finding global solutions can be significantly slower than finding local solutions.
- Gurobi can find global solutions to non-convex quadratic problems.
- For a free non-convex solver, you can try the popular nonlinear solver IPOPT e.g. using CasADi.
- A list of (convex/non-convex) quadratic programming software (not necessarily in Python) was compiled by Nick Gould and Phillip Toint.
- Unfortunately most available QP solvers are designed for convex problems (i.e. problems for which
- I get the following build error on Windows when running
pip install qpsolvers.- You will need to install the Visual C++ Build Tools to build all package dependencies.
- Can I help?
- Absolutely! The first step is to install the library and use it. Report any bug in the issue tracker.
- If you're a developer looking to hack on open source, check out the contribution guidelines for suggestions.
Benchmark
On a dense problem, the performance of all solvers (as measured by IPython's %timeit on an Intel(R) Core(TM) i7-6700K CPU @ 4.00GHz) is:
| Solver | Type | Time (ms) |
|---|---|---|
| qpswift | Dense | 0.008 |
| quadprog | Dense | 0.01 |
| qpoases | Dense | 0.02 |
| osqp | Sparse | 0.03 |
| scs | Sparse | 0.03 |
| ecos | Sparse | 0.27 |
| cvxopt | Dense | 0.44 |
| gurobi | Sparse | 1.74 |
| mosek | Sparse | 7.17 |
On a sparse problem with n = 500 optimization variables, these performances become:
| Solver | Type | Time (ms) |
|---|---|---|
| osqp | Sparse | 1 |
| qpswift | Dense | 2 |
| scs | Sparse | 4 |
| mosek | Sparse | 17 |
| ecos | Sparse | 33 |
| cvxopt | Dense | 51 |
| gurobi | Sparse | 221 |
| quadprog | Dense | 427 |
| qpoases | Dense | 1560 |
On a model predictive control problem for robot locomotion, we get:
| Solver | Type | Time (ms) |
|---|---|---|
| quadprog | Dense | 0.03 |
| qpswift | Dense | 0.08 |
| qpoases | Dense | 0.36 |
| osqp | Sparse | 0.48 |
| ecos | Sparse | 0.69 |
| scs | Sparse | 0.76 |
| cvxopt | Dense | 2.75 |
Finally, here is a small benchmark of random dense problems (each data point corresponds to an average over 10 runs):
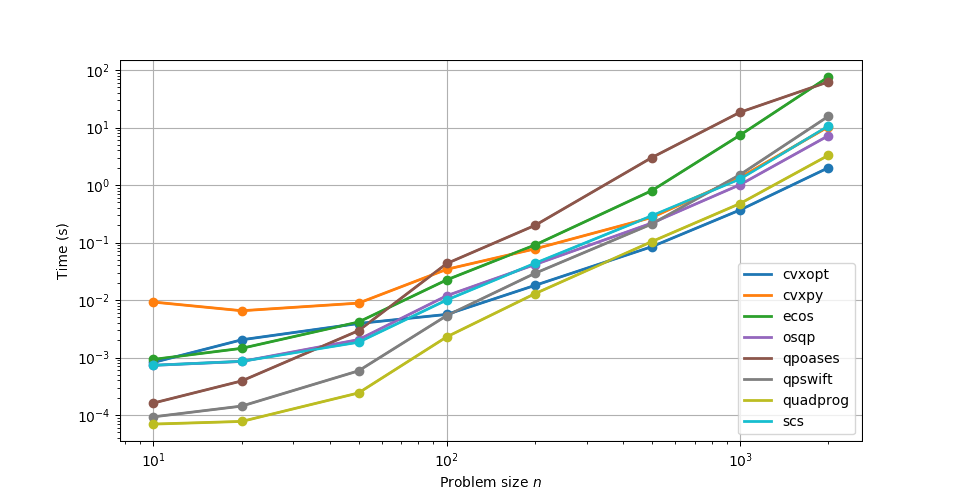
Note that performances of QP solvers largely depend on the problem solved. For instance, MOSEK performs an automatic conversion to Second-Order Cone Programming (SOCP) which the documentation advises bypassing for better performance. Similarly, ECOS reformulates from QP to SOCP and works best on small problems.
Contributing
We welcome contributions, see Contributing for details.
Project details
Release history Release notifications | RSS feed
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages.
Source Distribution
Built Distribution
File details
Details for the file qpsolvers-3.0.0.tar.gz.
File metadata
- Download URL: qpsolvers-3.0.0.tar.gz
- Upload date:
- Size: 74.1 kB
- Tags: Source
- Uploaded using Trusted Publishing? No
- Uploaded via: python-requests/2.26.0
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | bdc5ae94525f055147b81e1662399167730dd01de138aade0883c1d204da1624 |
|
| MD5 | 0ef1ae82e573243b1af872f6b42f8f06 |
|
| BLAKE2b-256 | a7aa1e4687a38f0d567655f69e0cc7799289edc7094388a65aff797f873741da |
File details
Details for the file qpsolvers-3.0.0-py3-none-any.whl.
File metadata
- Download URL: qpsolvers-3.0.0-py3-none-any.whl
- Upload date:
- Size: 66.0 kB
- Tags: Python 3
- Uploaded using Trusted Publishing? No
- Uploaded via: python-requests/2.26.0
File hashes
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | 17f09c76b9ccdd4c11e1ce199ae28d0e873a5b999ad940e5133f9d666d15f2fd |
|
| MD5 | 10d2bd6df6df524d709a4248f04f5d50 |
|
| BLAKE2b-256 | ac16bc3024f0e5f8456c8ac3cb77dac5c37b45c97882a94d931e24b1149b1330 |

















